
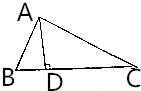
 △ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,求证:△ABC是直角三角形.
△ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,求证:△ABC是直角三角形. 分析 利用△ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,证明△ADC∽△BDA,可得∠ACD=∠BAD,即可证明结论.
解答 证明:∵△ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,
∴$\frac{1}{A{C}^{2}}$=$\frac{B{D}^{2}}{A{D}^{2}•A{B}^{2}}$,
∴$\frac{AD}{AC}$=$\frac{BD}{AB}$,
∴△ADC∽△BDA,
∴∠ACD=∠BAD,
∴∠BAD+∠CAD=∠ACD+∠CAD=90°,
∴AB⊥AC,
∴△ABC是直角三角形.
点评 本题考查三角形相似的判定与性质,考查学生分析解决问题的能力,证明三角形相似是关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
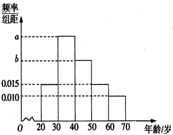 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
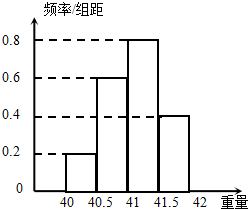 某工厂生产的200件产品的重量(单位:kg)的频率分布直方图如图所示,则重量在[40,41)的产品大约有( )
某工厂生产的200件产品的重量(单位:kg)的频率分布直方图如图所示,则重量在[40,41)的产品大约有( )| A. | 160件 | B. | 120件 | C. | 80件 | D. | 60件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) | |
| B. | 向右平移$\frac{π}{6}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| C. | 向左平移$\frac{π}{3}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| D. | 向左平移$\frac{π}{6}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com