
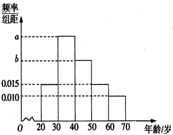
 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.分析 (1)直方图中,频率=组距×纵坐标及频率和为1,列出方程组;
(2)利用分层抽样从样本中抽取5人,其中年龄在[30,50)为3人,其余年龄段的为2人,取到所有的抽取情况及得代金卷总和为90元的情况列出,利用古典概型概率公式求出.
解答 解:(1)由已知可得$\left\{\begin{array}{l}{a+b=0.060}\\{a+0.015=2b}\end{array}\right.$,
解得:a=0.035,b=0.025.
(2)利用分层抽样从样本中抽取5人,其中年龄在[30,50)为3人,其余年龄段的为2人.
随机抽取3人,有${C}_{5}^{3}$=10种,此3人获得代金券的金额总和为90元,则需要2个20元和1个50元,有${C}_{3}^{2}{C}_{2}^{1}$=6种,
∴此3人获得代金券的金额总和为90元的概率为$\frac{6}{10}$=0.6.
点评 本小题主要考查统计与概率的相关知识.本题主要考查数据处理能力.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与a,b均相交 | B. | 与a,b都不相交 | ||
| C. | 至少与a,b中的一条相交 | D. | 至多与a,b中的一条相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
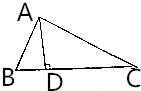 △ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,求证:△ABC是直角三角形.
△ABC中,AD⊥BC,且$\frac{1}{A{C}^{2}}$=$\frac{1}{A{D}^{2}}$-$\frac{1}{A{B}^{2}}$,求证:△ABC是直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6+3\sqrt{3}}{4}$ | B. | $\frac{3+\sqrt{3}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com