
分析 根据奇函数性质得出b=d=0,对a进行讨论,利用导数求出f(x)在[-1,1]上的单调性得出最值,根据fmax(x)≤1解出a的范围.
解答 解:∵f(x)是奇函数,∴f(-x)=-f(x),即-ax3+bx2-cx+d=-ax3-bx2-cx-d,
∴b=d=0.
∵f(1)=a+c=1,∴c=1-a.∴f(x)=ax3+(1-a)x.
∵f(x)是奇函数,且对任意的x∈[-1,1],都有|f(x)|≤1成立,
∴fmax(x)≤1,
f′(x)=3ax2+1-a,
(1)若a=0,则f(x)=x在[-1,1]上是增函数,∴fmax(x)=1,显然符合题意;
(2)若0<a≤1,则f′(x)≥0,∴f(x)在[-1,1]上是增函数,∴fmax(x)=f(1)=1,符合题意;
(3)若a>1,令f′(x)=0得x=±$\sqrt{\frac{a-1}{3a}}$,
∵$\frac{a-1}{3a}$=$\frac{1}{3}$-$\frac{1}{3a}$$<\frac{1}{3}$,
∴f(x)在[-1,-$\sqrt{\frac{a-1}{3a}}$]上单调递增,则(-$\sqrt{\frac{a-1}{3a}}$,$\sqrt{\frac{a-1}{3a}}$)上单调递减,在($\sqrt{\frac{a-1}{3a}}$,1]上单调递增.
∵f(1)=1,∴f(-$\sqrt{\frac{a-1}{3a}}$)≤1,即$\frac{2}{3}$(a-1)$\sqrt{\frac{a-1}{3a}}$≤1,解得1<a≤4.
(4)若a<0,令f′(x)=0得x=±$\sqrt{\frac{a-1}{3a}}$,
①若$\sqrt{\frac{a-1}{3a}}$<1,即a<-$\frac{1}{2}$,则f(x)在[-1,-$\sqrt{\frac{a-1}{3a}}$]上单调递减,则(-$\sqrt{\frac{a-1}{3a}}$,$\sqrt{\frac{a-1}{3a}}$)上单调递增,在($\sqrt{\frac{a-1}{3a}}$,1]上单调递减.
∵f(1)=1,∴fmax(x)>f(1)=1,不符合题意.
②若$\sqrt{\frac{a-1}{3a}}$≥1,即a≥-$\frac{1}{2}$,则f(x)在[-1,1]上单调递增,则fmax(x)=f(1)=1,符合题意;
综上,a的取值范围是[-$\frac{1}{2}$,4].
故答案为[-$\frac{1}{2}$,4].
点评 本题考查了导数与函数单调性的关系,奇函数的性质,函数最值的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x大大增大,y一定变大,z可能不变 | B. | x可能不变,y可能不变,z可能不变 | ||
| C. | x大大增大,y可能不变,z也不变 | D. | x大大增大,y可能不变,z变大 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
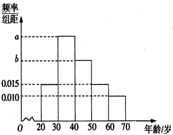 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45°或135° | B. | 135° | C. | 45° | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com