
分析 把3只红色乒乓球标记为A、B、C,3只白色的乒乓球标记为1、2、3.列出从6个球中随机摸出3个的基本事件.
(1)事件E={摸出的3个球为白球},事件E包含的基本事件有1个,然后求解概率.
(2)事件F={摸出的3个球为2个红球1个白球},事件F包含的基本事件有9个,求解概率即可.
解答 解:把3只红色乒乓球标记为A、B、C,3只白色的乒乓球标记为1、2、3.
从6个球中随机摸出3个的基本事件为:
ABC、AB1、AB2、AB3、AC1、
AC2、AC3、A12、A13、A23、
BC1、BC2、BC3、B12、B13、
B23、C12、C13、C23、123,共20个
(1)事件E={摸出的3个球为白球},
事件E包含的基本事件有1个,即摸出123:
P(E)=$\frac{1}{20}$=0.05
(2)事件F={摸出的3个球为2个红球1个白球},
事件F包含的基本事件有9个,
P(F)=$\frac{9}{20}$=0.45
点评 本题考查古典概型的概率的求法,列出所有的基本事件个数是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
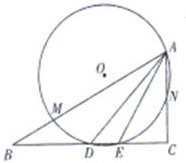 如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:
如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数F(x)=$\frac{f(x)}{x}$在(0,+∞)上为增函数 | B. | 函数F (x)=$\frac{f(x)}{x}$在(0,+∞)上为减函数 | ||
| C. | 函数G(x)=xf(x)在(0,+∞)上为增函数 | D. | 函数G(x)=xf(x)在(0,+∞)上为减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com