
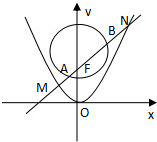
 已知点F是抛物线C:x2=2py(p>0)的焦点,点P(3,y0)(y0>1)是抛物线C上一点,且$|{PF}|=\frac{13}{4}$,⊙Q的方程为x2+(y-3)2=6,过点F作直线l,与抛物线C和⊙Q依次交于M,A,B,N.(如图所示)
已知点F是抛物线C:x2=2py(p>0)的焦点,点P(3,y0)(y0>1)是抛物线C上一点,且$|{PF}|=\frac{13}{4}$,⊙Q的方程为x2+(y-3)2=6,过点F作直线l,与抛物线C和⊙Q依次交于M,A,B,N.(如图所示)分析 (1)由P(3,y0)在抛物线C上得2py0=9,结合抛物线的定义,即可求抛物线C的方程;
(2)由题知直线l的斜率一定存在,设直线l的方程为y=kx+1,表示出(|MB|+|NA|)•|AB|,即可求(|MB|+|NA|)•|AB|的最小值.
解答 解:(1)由P(3,y0)在抛物线C上得2py0=9
又由$|{PF}|=\frac{13}{4}$得${y_0}+\frac{p}{2}=\frac{13}{4}$
解得$\left\{{\begin{array}{l}{{y_0}=1}\\{p=\frac{9}{2}}\end{array}}\right.$,$\left\{{\begin{array}{l}{{y_0}=\frac{9}{4}}\\{p=2}\end{array}}\right.$,又y0>1 故$\left\{{\begin{array}{l}{{y_0}=\frac{9}{4}}\\{p=2}\end{array}}\right.$
所以抛物线C的方程为x2=4y.…(4分)
(2)由题知直线l的斜率一定存在,设直线l的方程为y=kx+1
则圆心Q(0,3)到直线l的距离为$d=\frac{2}{{\sqrt{{k^2}+1}}}$,
∴$|{AB}|=2\sqrt{{r^2}-{d^2}}=2\sqrt{6-\frac{4}{{{k^2}+1}}}$…(6分)
设M(x1,y1),N(x2,y2),
由$\left\{{\begin{array}{l}{{x^2}=4y}\\{y=kx+1}\end{array}}\right.$得y2-(2+4k2)y+1=0,
则${y_1}+{y_2}=4{k^2}+2$,由抛物线定义知,$|MN|={y_1}+{y_2}+2=4(1+{k^2})$…(8分)
∴(|MB|+|NA|)•|AB|=(|MN|+|AB|)•|AB|=|MN||AB|+|AB|2
=$8({k^2}+1)\sqrt{(6-\frac{4}{{{k^2}+1}})}+4•(6-\frac{4}{{{k^2}+1}})$=$8\sqrt{6{{({k^2}+1)}^2}-4({k^2}+1)}-\frac{16}{{{k^2}+1}}+24$…(10分)
设t=k2+1(t≥1),则$(|{MB}|+|{NA}|)•|{AB}|=8\sqrt{6{t^2}-4t}-\frac{16}{t}+24=8\sqrt{6{{(t-\frac{1}{3})}^2}-\frac{2}{3}}-\frac{16}{t}+24$,(t≥1)
∵函数$y=\sqrt{6{{(t-\frac{1}{3})}^2}-\frac{2}{3}}$和$y=-\frac{16}{t}$在[1,+∞﹚上都是单调递增函数
∴当t=1时即k=0时,(|MB|+|NA|)•|AB|有最小值$8\sqrt{2}+8$.…(12分)
点评 本题考查抛物线的方程与定义,考查直线与抛物线的位置关系,考查函数思想的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{6+3\sqrt{3}}{4}$ | B. | $\frac{3+\sqrt{3}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
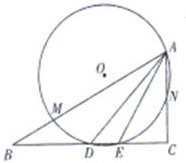 如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:
如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
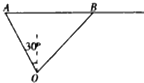 某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com