
分析 (1)分类讨论,解不等式,即可得出结论;
(2)由绝对值不等式可得f(x)的最大值为3,再利用基本不等式,即可证明结论.
解答 解:(1)当m=1时,f(x)=|x-2|-|x+1|.
x<-1时,f(x)=3,不符合题意;
-1≤x<2时,f(x)=-2x+1≤1,可得0≤x<2;
x≥2时,f(x)=-3≤1,符合题意;
∴不等式f(x)≤1的解集为[0,+∞);
证明:(2)由绝对值不等式可得|mx-2|-|mx+1|≤|mx-2-mx-1|=3,
∴f(x)的最大值为3,
∴n=3,a+b+c=3,
∴$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$≤$\frac{1+a}{2}$+$\frac{1+b}{2}$+$\frac{1+c}{2}$=3(当且仅当a=b=1时等号成立)
点评 本题考查绝对值不等式的解法,考查不等式的证明,考查基本不等式的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
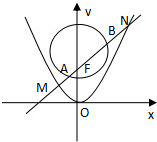 已知点F是抛物线C:x2=2py(p>0)的焦点,点P(3,y0)(y0>1)是抛物线C上一点,且$|{PF}|=\frac{13}{4}$,⊙Q的方程为x2+(y-3)2=6,过点F作直线l,与抛物线C和⊙Q依次交于M,A,B,N.(如图所示)
已知点F是抛物线C:x2=2py(p>0)的焦点,点P(3,y0)(y0>1)是抛物线C上一点,且$|{PF}|=\frac{13}{4}$,⊙Q的方程为x2+(y-3)2=6,过点F作直线l,与抛物线C和⊙Q依次交于M,A,B,N.(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4] | B. | [4,+∞) | C. | (-∞,-4]∪[4,+∞) | D. | (-∞,-4)∪(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
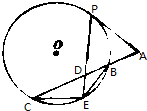 如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:
如图,已知PA与圆O相切,P为切点,割线ABC与圆O相切于点B,C,AC=2PA,D为AC的中点.PD的延长线交圆O于E点,证明:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com