
分析 分类讨论,当a=0时,求出直线l1和l2,当a≠0时,分别求出相对应的斜率,
(1)根据两直线平行关系,即斜率相等,且不重合即可求出a的值.
(2)根据两直线垂直的关系,即斜率乘积等于-1,即可求出a的值.
解答 解:(1)l1:x+ay-2a-2=0,l2:ax+y-1-a=0,
当a=0时,l1:x=2,l2:y=1,两直线垂直,
当a≠0时,k1=-$\frac{1}{a}$,k2=-a
(1)∵l1∥l2,
∴-$\frac{1}{a}$=-a,
解得a=±1,
当a=-1时,l1:x-y=0,l2:x-y=0,两直线重合,
∴a=1,
(2)∵l1⊥l2,
当a≠0时,(-$\frac{1}{a}$)•(-a)=-1,无解,
当a=0时,l1:x=2,l2:y=1,两直线垂直,
综上所述a=0
点评 本题考查两直线平行的性质,两直线垂直的性质,要特别注意直线的斜率不存在时的情况,要进行检验.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
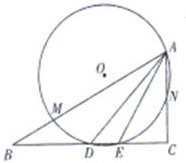 如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:
如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数F(x)=$\frac{f(x)}{x}$在(0,+∞)上为增函数 | B. | 函数F (x)=$\frac{f(x)}{x}$在(0,+∞)上为减函数 | ||
| C. | 函数G(x)=xf(x)在(0,+∞)上为增函数 | D. | 函数G(x)=xf(x)在(0,+∞)上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com