
(1)设 ,求证:
,求证: 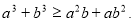
(2)已知正数x、y满足2x+y=1,求 的最小值及对应的x、y值.
的最小值及对应的x、y值.
(3)已知实数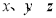 满足
满足 ,
, 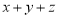 的最大值及对应的x、y、z值.
的最大值及对应的x、y、z值.
(1)见解析;
(2)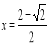 ,
,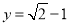 时
时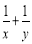 有最小值为
有最小值为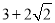 。
。
(3)当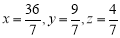 时,
时,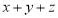 取最大值,所以
取最大值,所以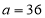 .
.
【解析】
试题分析:(1)法一,分析法:证明使a3+b3>a2b+ab2成立的充分条件成立,
法二,综合法:由条件a≠b推出:a2-2ab+b2>0,通过变形,应用不等式的性质可证出结论.(2)利用基本不等式求最值必须满足一正,二定,三相等三个条件,并且和为定值时,积有最大值,积为定值时,和有最小值(3)柯西不等式是一个非常重要的不等式,灵活巧妙的应用它,可以使一些较为困难的问题迎刃而解。可在证明不等式,解三角形相关问题,求函数最值,解方程等问题的方面得到应用,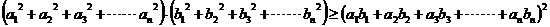 ,注意变形
,注意变形
试题解析:证明:法一:(分析法)
要证a2+b2>a2b+ab2成立,
只需证(a+b)(a2-ab+b2)>ab(a+b)成立
又因为a>0,
只需证a2-ab+b2>ab成立,
而依题设a≠b,则(a-b)2>0显然成立,
由此命题得证.
法二:(综合法)∵a≠b,
∴a-b≠0
∴a2-2ab+b2>0
∴a2-ab+b2>ab(*)
而a,b均为正数,
∴a+b>0,
∴(a+b)(a2-ab+b2)>ab(a+b)
∴a3+b3>a2b+ab2.
(2)因为正数x、y满足2x+y=1, 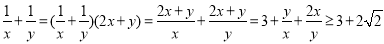
当且仅当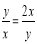 时取等号。 由
时取等号。 由 得
得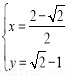 所以当
所以当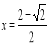 ,
,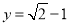 时
时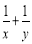 有最小值为
有最小值为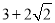 。
。
(3)解:由柯西不等式:
 .因为
.因为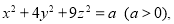 所以
所以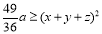 ,即
,即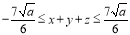 .因为
.因为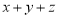 的最大值是7,所以
的最大值是7,所以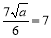 ,得
,得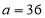 ,
,
当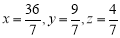 时,
时,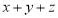 取最大值,所以
取最大值,所以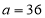 .
.
考点:作差法是比较两个代数式大小的与基本不等式及柯西不等式


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年福建省高一上学期第一次月考数学试卷(解析版) 题型:选择题
下列各组对象中,不能形成集合的是( )
A.连江五中全体学生 B.著名艺术家
C.目前获得诺贝尔奖的夫妇 D.高中数学的必修课本
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一阶段考试理科数学试卷(解析版) 题型:选择题
已知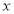 与
与 之间的几组数据如下表:
之间的几组数据如下表:
X | 0 | 1 | 2 | 3 |
y | 1 | 3 | 5 | 7 |
则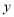 与
与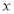 的线性回归方程
的线性回归方程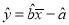 必过( )
必过( )
A.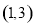 B.
B. C.
C.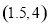 D.
D.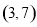
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一次检查文科数学试卷(解析版) 题型:选择题
若x,y满足约束条件 目标函数
目标函数 仅在点
仅在点 处取得最小值,则
处取得最小值,则 的取值范围是( )
的取值范围是( )
A.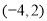 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
6人站成一排,甲、乙、丙3个人不能都站在一起的排法种数为( )
A.720 B.144 C.576 D.684
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com