已知集合A={x|x2+2x-8<0},B={x|x2>5-4x},C={x|m-1<x<m+1,m∈R}.
(Ⅰ)求A∩B;
(Ⅱ)若(A∩B)⊆C,求m的取值范围.
【答案】
分析:(Ⅰ)分别求出集合A和B中一元二次不等式不等式的解集,确定出集合A和B,找出两集合的公共元素即可得到两集合的交集;
(Ⅱ)由(A∩B)⊆C,得到(A∩B)为集合C的子集,列出关于m的不等式,求出不等式的解集即可得到m的取值范围.
解答:解:(Ⅰ)由集合A中的不等式x
2+2x-8<0,
变形得:(x-2)(x+4)<0,
可化为:
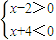
或

,
解得:-4<x<2,
∴集合A=(-4,2);
由集合B中的不等式x
2>5-4x,即x
2+4x-5>0,
变形得:(x-1)(x+5)>0,
可化为:
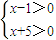
或
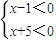
,
解得:x>1或x<-5,
∴集合B=(-∞,-5)∪(1,+∞),
在数轴上画出解集,如图所示:
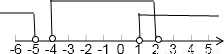
则A∩B=(1,2);
(2)∵(A∩B)⊆C,且A∩B=(1,2),C={x|m-1<x<m+1,m∈R},
∴
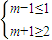
,
解得:1≤m≤2,
则m的取值范围为[1,2].
点评:此题是以一元二次不等式解集为平台,考查了交集的元素,以及集合间的包含关系,利用了数形结合的思想,是中考中常考的题型,此题本题还考查了集合中的参数取值问题,要求学生掌握两集合的包含关系,借助数轴列出相应的关于参数的不等式是解题的关键.

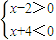 或
或 ,
,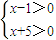 或
或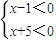 ,
,
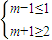 ,
,
