
已知函数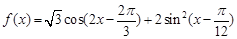 ,钝角
,钝角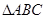 (角
(角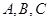 对边为
对边为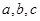 )的角
)的角 满足
满足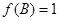 .
.
(1)求函数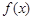 的单调递增区间;
的单调递增区间;
(2)若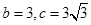 ,求
,求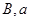 .
.
(1) ;(2)
;(2)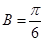 ,
, .
.
解析试题分析:(1)先用降幂公式将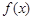 第二项化为
第二项化为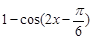 ,再利用两角和与差和余弦公式将两项展开合并同类型,再利用设辅助角公式化为一个角的三角函数,再利用正弦函数的单调性及复合函数同增异减法则求
,再利用两角和与差和余弦公式将两项展开合并同类型,再利用设辅助角公式化为一个角的三角函数,再利用正弦函数的单调性及复合函数同增异减法则求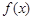 的单调增区间;(2)先利用利用大边对大角及
的单调增区间;(2)先利用利用大边对大角及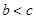 ,判断出角B为锐角,根据
,判断出角B为锐角,根据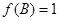 列出关于B的方程,求出B角,再利用余弦定理求出列出关于边
列出关于B的方程,求出B角,再利用余弦定理求出列出关于边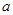 的方程,求出
的方程,求出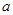 ,再利用余弦定理检验△ABC是否为钝角三角形,不是钝角三角形的
,再利用余弦定理检验△ABC是否为钝角三角形,不是钝角三角形的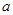 值舍去.
值舍去.
试题解析:(1)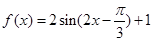 ,由
,由
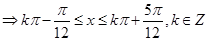 ,所以函数
,所以函数 的单调递增区间是
的单调递增区间是 .
.
(2)由

又因为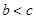 ,所以
,所以 ,故
,故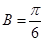
根据余弦定理,有 ,解得
,解得 或
或
又因为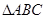 为钝角三角形,所以
为钝角三角形,所以 .
.
考点:1.两角和与差的三角公式及降幂公式;2.三角函数的单调性;3.余弦定理;4.运算求解能力.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
设a= ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数ω>0,若y=f(ωx)在区间 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;
(3)设集合A= ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A B,求实数m的取值范围.
B,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com