
如图,在正方体 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)设 为正方体
为正方体 棱上一点,给出满足条件
棱上一点,给出满足条件 的点
的点 的个数,并说明理由.
的个数,并说明理由.
(1)详见解析;(2)详见解析;(3)在正方体 棱上使得
棱上使得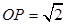 的点
的点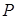 有12个.
有12个.
解析试题分析:(1)求证:平面 平面
平面 ,证明两平面垂直,只需证明一个平面过另一个平面的垂线,注意到本题是一个正方体,因此可证
,证明两平面垂直,只需证明一个平面过另一个平面的垂线,注意到本题是一个正方体,因此可证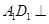 平面
平面 即可;(2)求证:
即可;(2)求证: 平面
平面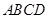 ,证明线面平行,即证线线平行,即在平面
,证明线面平行,即证线线平行,即在平面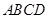 内找一条直线与
内找一条直线与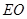 平行,注意到
平行,注意到 为
为 的中点,
的中点, 为
为 的中点,可连接
的中点,可连接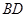 ,
,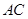 ,设
,设 ,连接
,连接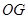 ,证明
,证明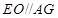 即可,即证四边形
即可,即证四边形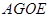 是平行四边形即可;(3)设
是平行四边形即可;(3)设 为正方体
为正方体 棱上一点,给出满足条件
棱上一点,给出满足条件 的点
的点 的个数,由(2)可知,
的个数,由(2)可知,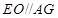 ,且
,且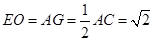 ,故点
,故点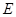 符合,有正方体的特征,可知,
符合,有正方体的特征,可知,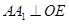 ,故
,故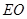 是点
是点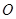 到
到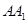 的最短距离,故这样的点就一个,同理在其他棱上各有一个,故可求出满足条件
的最短距离,故这样的点就一个,同理在其他棱上各有一个,故可求出满足条件 的点
的点 的个数.
的个数.
(1)在正方体 中,
中,
因为 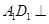 平面
平面 ,
,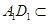 平面
平面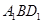 ,
,
所以平面 平面
平面 . 4分
. 4分
(2)证明:连接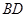 ,
,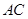 ,设
,设 ,连接
,连接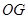 .
.
因为 为正方体,
为正方体,
所以 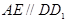 ,且
,且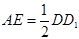 ,且
,且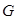 是
是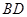 的中点,
的中点,
又因为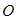 是
是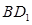 的中点,
的中点,
所以 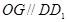 ,且
,且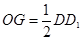 ,
,
所以 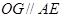 ,且
,且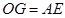 ,
,
即四边形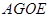 是平行四边形,
是平行四边形,
所以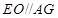 , 6分
, 6分
又因为 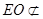 平面
平面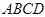 ,
,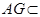 平面
平面 ,
,
所以  平面
平面

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:解答题
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90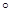 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为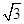 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1。
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB= 60°,FC⊥平面ABCD,AE⊥BD,CB=" CD=" CF.
(1)求证:BD⊥平面AED;
(2)求二面角F—BD—C的正切值.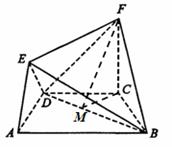
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2011•浙江)如图,在三棱锥P﹣ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=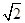 .
.
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com