
分析 根据函数奇偶性,单调性和最值的性质分别进行判断即可得到结论.
解答 解:①函数的定义域为(-∞,+∞),
则f(-x)=1-$\frac{1}{2}$cos(-x)-($\frac{1}{2}$)|-x|=1-$\frac{1}{2}$cosx-($\frac{1}{2}$)|x|=f(x),
则函数f(x)是偶函数,故①错误,
②当x=1000π=1000π时,满足x>2006,
此时f(1000π)=1-$\frac{1}{2}$cos1000π-($\frac{1}{2}$)|1000π|=$\frac{1}{2}$-($\frac{1}{2}$)|1000π|<$\frac{1}{2}$,
此时f(x)>$\frac{1}{2}$不成立,故②错误,
③∵$\frac{1}{2}$≤1-$\frac{1}{2}$cosx≤$\frac{3}{2}$,-1≤-($\frac{1}{2}$)|x|<0,
∴,-$\frac{1}{2}$<1-$\frac{1}{2}$cosx-($\frac{1}{2}$)|x|<$\frac{3}{2}$,取不到$\frac{3}{2}$,
故f(x)的最大值是$\frac{3}{2}$错误,故③错误,
④当x=0时,$\frac{1}{2}$cosx,($\frac{1}{2}$)|x|,同时取得最大值,
此时f(x)取得最小值f(0)=1-$\frac{1}{2}$-($\frac{1}{2}$)0=$\frac{1}{2}$,
即④f(x)的最小值是$\frac{1}{2}$.
故④正确,
故答案为:④.
点评 本题主要考查命题的真假判断,涉及函数的奇偶性,最值,单调性的性质,考查函数性质的综合应用.


科目:高中数学 来源: 题型:选择题
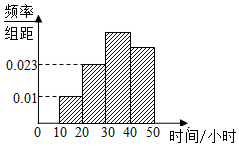 为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [1,+∞) | C. | (-∞,1] | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com