已知函数f(x)=4x+a•2x+1+4
(1)当a=1时,求函数f(x)的值域;
(2)若关于x的方程f(x)=0有两个大于0的实根,求a的取值范围;
(3)当x∈[1,2]时,求函数f(x)的最小值.
解:(1)设t=2
x>0,则y=g(t)=t
2+2at+4,
当a=1时,y=t
2+2t+4=(t+1)
2+3,对称轴为t=-1,开口向上.
∴g(t)在(0,+∞)上单调递增,∴g(t)>g(0)=4.
∴函数f(x)值域为(4,+∞).
(2)由x>0得t>1.
∴方程f(x)=0有两个大于0的实根等价于方程g(t)=t
2+2at+4=0有两个大于1的实根,
则需

解得
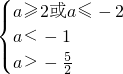
,
∴
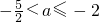
.
(3)由x∈[1,2]得t∈[2,4],g(t)=(t+a)
2+4-a
2.
①当-a≥4,即a≤-4时,g(t)在[2,4]上单调递减,
∴g(t)
min=g(4)=20+8a;
②当2<-a<4,-4<a<-2时,
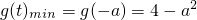
;
③当-a≤2即a≥-2时,g(t)在[2,4]上单调递增,
∴g(t)
min=g(2)=8+4a.
分析:(1)设t=2
x>0,则y=g(t)=t
2+2at+4,转化为求函数g(t)(t>0)的值域即可;
(2)由x>0得t>1,方程f(x)=0有两个大于0的实根?方程g(t)=t
2+2at+4=0有两个大于1的实根,求出即可;
(3)由x∈[1,2]得t∈[2,4],而g(t)=(t+a)
2+4-a
2,因此需要对-a与2、4的大小关系进行分类讨论即可.
点评:利用换元法和对所给的区间与二次函数的顶点的横坐标的关系分类讨论其单调性是解决问题的关键.

 解得
解得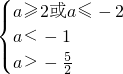 ,
,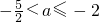 .
.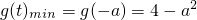 ;
;
