练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，在五棱锥S—ABCDE中，SA⊥底面ABCDE，SA=AB=AE=2，BC=DE=，∠BAE=∠BCD=∠CDE=120°.?

    (1)求异面直线CD与SB所成的角(用反三角函数值表示)；?

    (2)证明BC⊥平面SAB；?

    (3)用反三角函数值表示二面角B-SC-D的大小.(本小问不必写出解答过程)

    (1)解析：连结BE，延长BC、ED交于点F，则∠DCF=∠CDF=60°，∴△CDF为正三角形.∴CF=DF.

    又BC=DE，∴BF=EF.?

    因此，△BFE为正三角形.?

    ∴∠FBE=∠FCD=60°.?

    ∴BE∥CD.?

    所以∠SBE(或其补角)就是异面直线CD与SB所成的角.?

    ∵SA⊥底面ABCDE，SA=AB=AE=2，∴SB=2.?

    同理SE=2.?

    又∠BAE=120°，所以BE=2.?

    从而cos∠SBE=,?

    ∴∠SBE=arccos.?

    所以异面直线CD与SB所成的角是arccos.?

    (2)证明：由题意，△ABE为等腰三角形，∠BAE=120°,?

    ∴∠ABE=30°.?

    又∠FBE=60°，?

    ∴∠ABC=90°.?

    ∴BC⊥BA.?

    ∵SA⊥底面ABCDE，BC底面ABCDE ，∴SA⊥BC.?

    又SA∩BA=A,∴BC⊥平面SAB.?

    (3)解析：二面角BSCD的大小为π-arccos.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

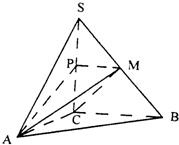    精英家教网如图，在三棱锥S-ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°．
    （1）求证：平面MAP⊥平面SAC．
    （2）求二面角M-AC-B的平面角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

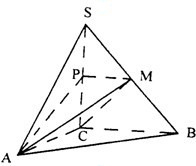    如图，在三棱锥S-ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°．
    （1）求证：BC∥面AMP；
    （2）求证：平面MAP⊥平面SAC；
    （3）求锐二面角M-AB-C的大小的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

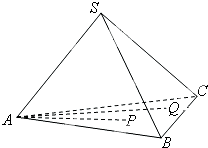    如图，在三棱锥S-ABC中，设P、Q为底面△ABC内的两点，且
    AP
    =
    2
    5
    AB
    +
    1
    5
    AC
    ，
    AQ
    =
    2
    3
    AB
    +
    1
    4
    AC
    ，则VS-ABP：VS-ABQ=
    4
    5
    4
    5
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

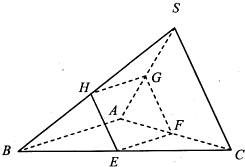    （2012•江苏二模）如图，在三棱锥S-ABC，平面EFGHBC，CA，AS，SB交与点E，F，G，H，且SA⊥平面EFGH，SA⊥AB，EF⊥FG．
    （1）AB∥平面EFGH；
    （2）GH∥EF；
    （3）GH⊥平面SAC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•杭州模拟）如图，在三棱锥S-ABC中，SA=SC=AB=BC，则直线SB与AC所成角的大小是（　　）

    查看答案和解析>>

    同步练习册答案