
【题目】如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,将
的中点,将![]() 分别沿
分别沿![]() ,
,![]() 折起,使
折起,使![]() 两点重合于
两点重合于![]() .
.

(Ⅰ)求证:平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)证明面面垂直,一般利用面面垂直判定定理,即从线面垂直出发给予证明,而线面垂直的证明往往利用线面垂直判定与性质定理,即从线线垂直出发给予证明,而线线垂直的寻找与论证往往需结合平几知识进行:连接![]() 交
交![]() 于
于![]() ,则根据等腰三角形性质得
,则根据等腰三角形性质得![]() ,
,![]() (Ⅱ)求二面角,一般利用空间向量进行求解,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与向量夹角之间关系求解
(Ⅱ)求二面角,一般利用空间向量进行求解,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与向量夹角之间关系求解
试题解析:(Ⅰ)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.

在正方形![]() 中,点
中,点![]() 是
是![]() 中点,点
中点,点![]() 是
是![]() 中点,
中点,
所以![]() ,
,
所以![]() ,
,
所以在等腰![]() 中,
中,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
因此在等腰![]() 中,
中,![]() ,
,
从而![]() ,
,
又![]() ,
,
所以平面![]() ,
,
即平面![]() .…………………6分
.…………………6分
(Ⅱ)方法一:

在正方形![]() 中,连接
中,连接![]() ,交
,交![]() 于
于![]() ,设正方形
,设正方形![]() 的边长为2,
的边长为2,
由于点![]() 是
是![]() 中点,点
中点,点![]() 是
是![]() 中点,
中点,
所以![]() ,
,
于是![]() ,
,
从而![]() ,
,
所以![]() ,
,
于是,在翻折后的几何体中,![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在正方形![]() 中,解得
中,解得![]() ,
,![]() ,
,
所以,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,
所以,二面角![]() 的余弦值为
的余弦值为![]() .………………………………12分
.………………………………12分
方法二:
由题知![]() 两两互相垂直,故以
两两互相垂直,故以![]() 为原点,向量
为原点,向量![]() 方向分别为
方向分别为![]() ,
,![]() ,
,![]() 轴的正方向,建立如图的空间直角坐标系.
轴的正方向,建立如图的空间直角坐标系.
设正方形边长为2,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由 得
得![]() ,
,
令![]() ,得
,得![]() ,
,
又由题知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以![]() .
.
所以,二面角![]() 的余弦值为
的余弦值为![]() .………………………………12分
.………………………………12分



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在各棱长为![]() 的直四棱柱
的直四棱柱![]() 中,底面
中,底面![]() 为棱形,
为棱形, ![]() 为棱
为棱![]() 上一点,且
上一点,且![]()

(1)求证:平面![]() 平面
平面![]() ;
;
(2)平面![]() 将四棱柱
将四棱柱![]() 分成上、下两部分,求这两部分的体积之比.
分成上、下两部分,求这两部分的体积之比.
(棱台的体积公式为![]() ,其中
,其中![]() 分别为上、下底面面积,
分别为上、下底面面积, ![]() 为棱台的高)
为棱台的高)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() +
+![]() =1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
=1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
(1)求椭圆E的方程;
(2)若MN是椭圆E经过 原点的弦,MN||AB,求证: ![]() 为定值
为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() ,并且经过
,并且经过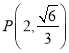 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
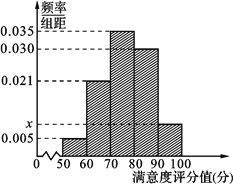
(1) 求图中![]() 的值;
的值;
(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”是个广为流传的游戏,游戏时甲乙双方每次做“石头”“剪刀”“布”三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛,假设甲乙两人都是等可能地做这三种手势.
(1)列举一次比赛时两人做出手势的所有可能情况;
(2)求一次比赛甲取胜的概率,并说明“石头、剪刀、布”这个广为流传的游戏的公平性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com