
| A. | -$\frac{4}{5}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{13}$ | D. | $\frac{13}{4}$ |
分析 根据题意,设等差数列{$\frac{1}{{a}_{n}}$}的公差为d,结合题意可得$\frac{1}{{a}_{1}}$=1,$\frac{1}{{a}_{4}}$=$\frac{1}{4}$,计算可得公差d的值,进而由等差数列的通项公式可得$\frac{1}{{a}_{10}}$的值,求其倒数可得a10的值.
解答 解:根据题意,{$\frac{1}{{a}_{n}}$}是等差数列,设其公差为d,
若a1=1,a4=4,有$\frac{1}{{a}_{1}}$=1,$\frac{1}{{a}_{4}}$=$\frac{1}{4}$,
则3d=$\frac{1}{{a}_{4}}$-$\frac{1}{{a}_{1}}$=-$\frac{3}{4}$,即d=-$\frac{1}{4}$,
则$\frac{1}{{a}_{10}}$=$\frac{1}{{a}_{1}}$+9d=-$\frac{5}{4}$,
故a10=-$\frac{4}{5}$;
故选:A.
点评 本题考查等差数列的通项公式,注意求出{$\frac{1}{{a}_{n}}$}的公差.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
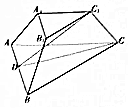 已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.
已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
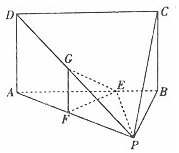 在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE:EB=7:2,点F、G分别为线段PA、PD的中点.
在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE:EB=7:2,点F、G分别为线段PA、PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
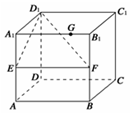 在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.
在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com