
分析 利用正弦定理求出c,利用余弦定理以及基本不等式求出ab的范围,然后求解三角形的面积.
解答 解:因为$C=\frac{π}{6}$,又$\frac{c}{sinC}=\frac{b}{sinB}=4\sqrt{3}$,得${c}=2\sqrt{3}$,
而${c^2}={a^2}+{b^2}-2abcosC={a^2}+{b^2}-\sqrt{3}ab≥({2-\sqrt{3}})ab$,
所以$ab≤\frac{12}{{({2-\sqrt{3}})}}=12({2+\sqrt{3}})$,当且仅当$a=b=\sqrt{12({2+\sqrt{3}})}$时等号成立,
即${S_{△ABC}}=\frac{1}{2}absinC=\frac{1}{4}ab≤3({2+\sqrt{3}})=6+3\sqrt{3}$,即当$a=b=\sqrt{12({2+\sqrt{3}})}$时,
三角形ABC面积最大值为$6+3\sqrt{3}$.
故答案为:6+3$\sqrt{3}$.
点评 本题考查三角形的解法,正弦定理以及余弦定理的应用,基本不等式的应用,考查转化思想以及计算能力.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{13}$ | D. | $\frac{13}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos201.2° | B. | -cos201.2° | C. | sin201.2° | D. | tan201.2° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
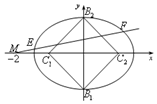 已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.
已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
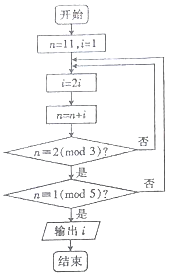 若正整数N除以正整数m后的余数为n,则记为N=n(mod m),例如10=2(mod 4),下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的i等于( )
若正整数N除以正整数m后的余数为n,则记为N=n(mod m),例如10=2(mod 4),下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的i等于( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com