
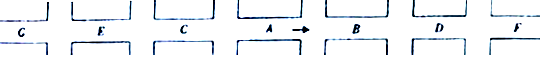
分析 (1)设小波遇到4次绿灯之后处于D街区为事件A,则事件A共有三个基本事件,由此能求出小波遇到4次绿灯后,处于D街区的概率.
(2)ξ可能的取值为0,1,2,3,分别求出相应的概率,由此能求出ξ分布列和数学期望.
解答 解:(1)设小波遇到4次红绿灯之后处于D街区为事件A,
则事件A共有三个基本事件,
即四次遇到的红绿灯情况分别为{红红绿绿,绿红红绿,绿绿红红}.
故$P(A)=3×{(\frac{2}{3})^2}×{(\frac{1}{3})^2}=\frac{4}{27}$.
(2)ξ可能的取值为0,1,2,3,
$P(ξ=0)={(\frac{1}{3})^3}+\frac{2}{3}×\frac{1}{3}×\frac{2}{3}=\frac{5}{27}$,
$P(ξ=1)=\frac{2}{3}×\frac{1}{3}×\frac{1}{3}+\frac{1}{3}×\frac{1}{3}×\frac{2}{3}+\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{6}{27}$,
$P(ξ=1)=\frac{2}{3}×\frac{2}{3}×\frac{1}{3}+\frac{1}{3}×\frac{2}{3}×\frac{2}{3}=\frac{8}{27}$,
$P(ξ=3)={(\frac{2}{3})^3}=\frac{8}{27}$.
故分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{5}{27}$ | $\frac{6}{27}$ | $\frac{8}{27}$ | $\frac{8}{27}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,在历年高考中都是必考题型之一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
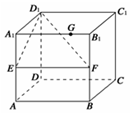 在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.
在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $9\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com