
【题目】已知直线![]() 为椭圆
为椭圆![]() 的右准线,直线
的右准线,直线![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,过右焦点
,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点.
两点.
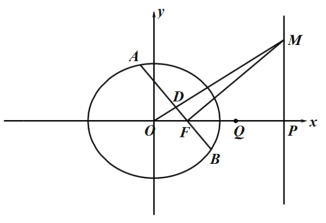
(1)设点![]() 在直线上,且满足
在直线上,且满足![]() ,若直线
,若直线![]() 与线段
与线段![]() 交于点
交于点![]() ,求证:点
,求证:点![]() 为线段
为线段![]() 的中点;
的中点;
(2)设![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试问
,试问![]() 是否为定值,若是,求出这个定值,若不是,请说明理由.
是否为定值,若是,求出这个定值,若不是,请说明理由.
【答案】(1)证明见解析; (2)![]() 为定值0.
为定值0.
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() , 故直线
, 故直线![]() 的方程为
的方程为![]() .再联立椭圆方程和直线
.再联立椭圆方程和直线![]() ,根据韦达定理求出线段
,根据韦达定理求出线段![]() 的中点为
的中点为![]() ,满足直线
,满足直线![]() 方程
方程![]() ,所以,直线
,所以,直线![]() 与线段
与线段![]() 交点
交点![]() 为线段
为线段![]() 的中点.
的中点.
(2)当直线![]() 的斜率为0时,
的斜率为0时, ![]() . 直线
. 直线![]() 的斜率不为0时,计算直线
的斜率不为0时,计算直线![]() 的方程,求得点
的方程,求得点![]() 的坐标为
的坐标为![]() ,纵坐标与点
,纵坐标与点![]() 相等,即
相等,即![]() ,
,![]() .
.
(1)由椭圆方程为![]() 知,右焦点
知,右焦点![]() 坐标
坐标![]() ,椭圆
,椭圆![]() 的右准线
的右准线![]() 方程为
方程为![]() ,点
,点![]() 坐标
坐标![]() .
.
①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与线段
与线段![]() 交点
交点![]() 即为右焦点
即为右焦点![]() ,此时点
,此时点![]() 为线段
为线段![]() 的中点.
的中点.
②又由![]() 知,直线
知,直线![]() 的斜率不为0,故设直线
的斜率不为0,故设直线![]() 的方程为
的方程为![]() ,
,
从而,直线![]() 的方程为
的方程为![]() ,令
,令![]() 得,
得,![]() 点坐标为
点坐标为![]() ,
,
故直线![]() 的方程为
的方程为![]() .
.
联立方程组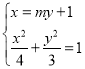 ,消去
,消去![]() 得:
得:![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
即![]() ,
,![]() ,
,
从而,线段![]() 的中点
的中点![]() .
.
又线段![]() 的中点
的中点![]() 的坐标满足直线
的坐标满足直线![]() 方程
方程![]() ,
,
所以,直线![]() 与线段
与线段![]() 交点
交点![]() 为线段
为线段![]() 的中点.
的中点.
综上可知,点![]() 为线段
为线段![]() 的中点.
的中点.
(2)当直线![]() 的斜率为0时,点
的斜率为0时,点![]() 即为点
即为点![]() ,从而
,从而![]() ,故
,故![]() .
.
直线![]() 的斜率不为0时,
的斜率不为0时,
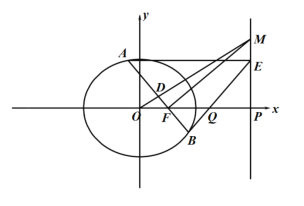
由(1)知,![]() ,
,![]() ,
,
所以![]() ,则
,则![]() .
.
直线![]() 的方程为
的方程为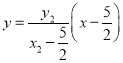 ,又
,又![]() ,
,
令![]() ,得
,得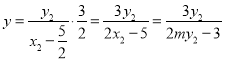
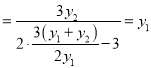 ,
,
所以点![]() 的坐标为
的坐标为![]() ,纵坐标与点
,纵坐标与点![]() 相等。
相等。
即![]() ,所以
,所以![]() .
.
综上可知,![]() 为定值0.
为定值0.


科目:高中数学 来源: 题型:
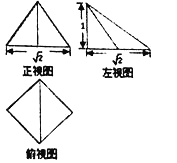
【题目】刘徽《九章算术商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]()
![]()
![]() 的左、右焦点,点P是以
的左、右焦点,点P是以![]() 为直径的圆与C在第一象限内的交点,若线段
为直径的圆与C在第一象限内的交点,若线段![]() 的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
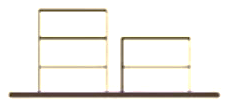
【题目】如图,在地上有同样大小的 5 块积木,一堆 2 个,一堆 3 个,要把积木一块一块的全部放到某个盒子里,每次 只能取出其中一堆最上面的一块,则不同的取法有______种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() (
(![]() )个单位长度后得到函数
)个单位长度后得到函数![]() 的图象,且函数
的图象,且函数![]() 的最大值为2.
的最大值为2.
(ⅰ)求函数![]() 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数
的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 经过点
经过点![]() ,两条渐近线的夹角为
,两条渐近线的夹角为![]() ,直线
,直线![]() 交双曲线于
交双曲线于![]() 、
、![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若![]() 过原点,
过原点,![]() 为双曲线上异于
为双曲线上异于![]() 、
、![]() 的一点,且直线
的一点,且直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 过双曲线的右焦点
过双曲线的右焦点![]() ,是否存在
,是否存在![]() 轴上的点
轴上的点![]() ,使得直线
,使得直线![]() 绕点
绕点![]() 无论怎样转动,都有
无论怎样转动,都有![]() 成立?若存在,求出
成立?若存在,求出![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com