
| A. | ①② | B. | ①③ | C. | ③④ | D. | ②③④ |
分析 ①,若α∥β,m?α,n?β,则m∥n或异面;
②,若m,n?α,m∥β,n∥β且m、n相交,则α∥β;
③,若m,n是两条异面直线,若m∥α,n∥α,在平面α内一定存在两条平行m、n的相交直线,由面面平行的判定可知α∥β;
④,如果m⊥α,m垂直平面α内及与α平行的直线,故m⊥n;
解答 解:对于①,若α∥β,m?α,n?β,则m∥n或异面,故错;
对于②,若m,n?α,m∥β,n∥β且m、n相交,则α∥β,故错;
对于③,若m,n是两条异面直线,若m∥α,n∥α,在平面α内一定存在两条平行m、n的相交直线,由面面平行的判定可知α∥β,故正确;
对于④,如果m⊥α,m垂直平面α内及与α平行的直线,故m⊥n,故正确;
故选:C
点评 本题考查了空间线线,线面,面面的位置关系,属于基础题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
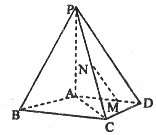 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-3)2+(y+4)2=3 | B. | (x-3)2+(y-4)2=3 | C. | (x+3)2+(y-4)2=3 | D. | $(x+3{)^2}+(y-4{)^2}=\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com