练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （几何证明选讲）（本小题满分10分）如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，求证：AB·CD = BC·DE．

     

     

    详见解析

    【解析】

    试题分析：根据题意结合圆的性质，由相交弦定理，得AC·CD = MC·NC，和BC·CE = MC·NC．化简即可得：AC·CD = BC·CE，对其整理即可（AB  BC）·CD = BC·（CD  DE），也即AB·CD  BC·CD = BC·CD  BC·DE，问题得证.

    试题解析：证明：由相交弦定理，得

    AC·CD = MC·NC．

    BC·CE = MC·NC．

    ∴AC·CD = BC·CE．

    即（AB  BC）·CD = BC·（CD  DE）．

    也即AB·CD  BC·CD = BC·CD  BC·DE．

    ∴AB·CD = BC·DE．

    考点：圆的相交弦定理

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届江西省高三上学期第三次考试理科数学试卷（解析版） 题型：选择题

    在△ABC中，已知，，则的值为（ ）

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省连云港高二下学期期末数学试卷（选修物理）（解析版） 题型：填空题

    若离散型随机变量X~B（6,p），且，则p＝ ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省连云港高二下学期期末数学试卷（选修历史）（解析版） 题型：填空题

    已知函数在区间上是单调减函数，则实数的取值范围是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省苏州市高三上学期期中测试数学试卷（解析版） 题型：解答题

    （本小题满分10分）某校要进行特色学校评估验收，有甲、乙、丙、丁、戊五位评估员将随机去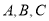三个不同的班级进行随班听课，要求每个班级至少有一位评估员．

    （1）求甲、乙同时去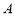班听课的概率；

    （2）设随机变量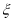为这五名评估员去班听课的人数，求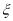的分布列和数学期望．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省苏州市高三上学期期中测试数学试卷（解析版） 题型：解答题

    （本题满分14分）已知△的面积为，且．

    （1）求的值；

    （2）若，，求△ABC的面积．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省苏州市高三上学期期中测试数学试卷（解析版） 题型：填空题

    已知直线与在点处的切线互相垂直，则 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届广东省深圳市高三上学期第一次五校联考理科数学试卷（解析版） 题型：填空题

    若不等式的解集是区间的子集，则实数的范围为__________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届广东省高三上学期暑假联考理科数学试卷（解析版） 题型：填空题

    已知圆的极坐标方程为，则该圆的圆心到直线 的距离是 .

     

    查看答案和解析>>

    同步练习册答案