
(2014•马鞍山二模)定义域为R的函数f(x),满足f(0)=1,f′(x)<f(x)+1,则不等式f(x)+1<2ex的解集为( )
A.{x∈R|x>1} B.{x∈R|0<x<1} C.{x∈R|x<0} D.{x∈R|x>0}
科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考理科数学试卷(解析版) 题型:选择题
已知双曲线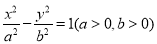 与抛物线
与抛物线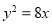 有一个公共的焦点
有一个公共的焦点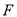 ,且两曲线的一个交点为
,且两曲线的一个交点为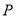 ,若
,若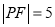 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
(A)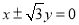
(B)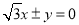
(C)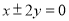
(D)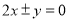
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-3 8.4列联表独立性分析案例练习卷(解析版) 题型:?????
(2013•江西一模)甲、乙两名棋手比赛正在进行中,甲必须再胜2盘才最后获胜,乙必须再胜3盘才最后获胜,若甲、乙两人每盘取胜的概率都是 ,则甲最后获胜的概率是( )
,则甲最后获胜的概率是( )
A.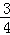 B.
B.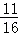 C.
C.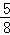 D.
D.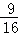
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-3 8.4列联表独立性分析案例练习卷(解析版) 题型:?????
(2014•黄山二模)甲、乙两名考生在填报志愿时都选中了A、B、C、D四所需要面试的院校,这四所院校的面试安排在同一时间,因此甲、乙都只能在这四所院校中选择一所做志愿,假设每位同学选择各个院校是等可能的,则甲、乙选择同一所院校的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•浙江模拟)已知f(x)为R上的可导函数,且满足f(x)>f′(x),对任意正实数a,下面不等式恒成立的是( )
A.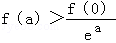
B.
C.f(a)>eaf(0)
D.f(a)<eaf(0)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•重庆三模)对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=
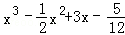 ,则g(
,则g(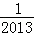 )+
)+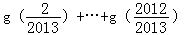 =( )
=( )
A.2011 B.2012 C.2013 D.2014
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
已知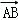 =(1,5,﹣2),
=(1,5,﹣2),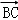 =(3,1,z),若
=(3,1,z),若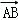 ⊥
⊥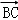 ,
,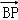 =(x﹣1,y,﹣3),且BP⊥平面ABC,则实数x、y、z分别为( )
=(x﹣1,y,﹣3),且BP⊥平面ABC,则实数x、y、z分别为( )
A.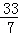 ,﹣
,﹣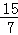 ,4 B.
,4 B.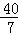 ,﹣
,﹣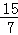 ,4 C.
,4 C.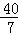 ,﹣2,4 D.4,
,﹣2,4 D.4,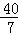 ,﹣15
,﹣15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com