
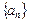 是公比为q的无穷等比数列,下列
是公比为q的无穷等比数列,下列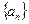 的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号).①S1与S2;②a2与S3;③a1与an;④q与an.(其中n为大于1的整数,Sn为
的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号).①S1与S2;②a2与S3;③a1与an;④q与an.(其中n为大于1的整数,Sn为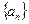 的前n项和.)
的前n项和.) 可得公比q,故能确定数列是该数列的“基本量”.
可得公比q,故能确定数列是该数列的“基本量”.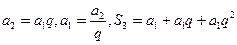
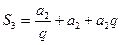 ,∴
,∴
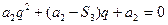
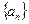 的基本量.
的基本量.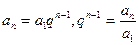 ,当n为奇数时,q可能有两个值,故不一定能确定数列,所以也不一定是数列的一个基本量.
,当n为奇数时,q可能有两个值,故不一定能确定数列,所以也不一定是数列的一个基本量.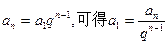 ,故数列
,故数列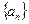 能够确定,是数列
能够确定,是数列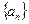 的一个基本量.故应填①、④
的一个基本量.故应填①、④

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com