练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知正数a、b、c满足a+b+c=1，求证：（1-a）
    		a
    ≤
    2
    		3
    9
    ．
    考点：不等式的证明
    专题：证明题
    分析：依题意知，0＜a＜1，令y=（1-a）
    		a
    ，可求得y2=（1-a）2a=
    1
    2
    ×2a（1-a）（1-a），利用基本不等式2a（1-a）（1-a）≤[
    2a+(1-a)+(1-a)
    3
    ]    3    =
    4
    27
    ，再开方即可证得结论．
    解答： 解：∵a+b+c=1，a，b，c为正数，∴0＜a＜1，
    令y=（1-a）
    		a
    ，
    则y2=（1-a）2a=
    1
    2
    ×2a（1-a）（1-a）
    ≤
    1
    2
    ×[
    2a+(1-a)+(1-a)
    3
    ]    3    =
    4
    27
    ，
    ∴y≤
    2
    		3
    9
    ，即（1-a）
    		a
    ≤
    2
    		3
    9
    ．
    点评：本题考查不等式的证明，考查构造函数思想，利用基本不等式2a（1-a）（1-a）≤[
    2a+(1-a)+(1-a)
    3
    ]    3    =
    4
    27
    是关键，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    复数z的虚部为1，且
    z
    1+i
    为纯虚数，其中i是虚数单位，则z=（　　）
    A、-1-iB、1+i
    C、1-iD、-1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）=ax3+bx2+c的图象经过点（0，1），且在x=1处的切线方程是y=-2x+1
    （1）求y=f（x）的解析式；
    （2）求y=f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}满足
    an+1
    an
    =q，且q≠0，数列{bn}满足bn=na1+（n-1）a2+（n-2）a3+…+2an-1+an（n∈N*），已知b1=m，b2=
    3m
    2
    ，其中m≠0：
    （Ⅰ）当m=1时，求bn；
    （Ⅱ）设Sn为数列{an}的前n项和，若对于任意的正整数n，都有Sn2-4sn+3≤0恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

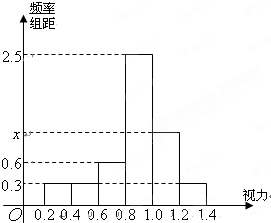    为了解某校高三学生的视力情况，随机抽查了该校50名高三学生，得到如图所示的频率分布直方图．
    （Ⅰ）求图中x的值；
    （Ⅱ）若从视力在[0.2，0.6）的学生中随机选取2人，求这2人视力均在[0.2，0.4）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

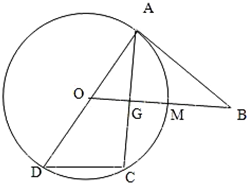    如图所示，已知AD为圆O的直径，直线BA与圆O相切于点A，直线OB与弦AC垂直并相交于点G，与弧AC相交于M，连接DC，AB=10，AC=12，则BM=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于以下结论：
    ①若y=f（x）是奇函数，则f（0）=0；
    ②已知p：事件A、B是对立事件，q：事件A、B是互斥事件，则p是q的必要但不充分条件；
    ③
    ln5
    5
    ＜
    ln3
    3
    ＜
    1
    e
    （e为自然对数的底数）；
    ④若
    a
    =（1，2），
    b
    =（0，-1），则
    b
    在
    a
    上的投影为
    2
    		5
    5
    ；
    ⑤若随机变量ξ～N（1，4），则P（ξ≤1）=
    1
    2
    ．
    其中，正确结论的序号为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

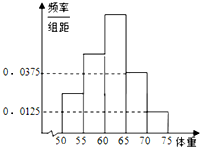    为了了解高三学生的身体状况，抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图（如图）．已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为15，则抽取的男生总人数是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    化简：
    cos15°-2sin15°
    sin15°
    =
     
    ．

    查看答案和解析>>

    同步练习册答案