
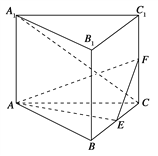
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.
【答案】(1)见解析(2)![]()
【解析】(1)证明:如图,因为三棱柱ABC-A1B1C1是直三棱柱,所以AE⊥BB1,
又E是正三角形ABC的边BC的中点,所以AE⊥BC,因此AE⊥平面B1BCC1,又AE平面AEF,所以平面AEF⊥平面B1BCC1.

(2)设AB的中点为D,连接A1D,CD,因为△ABC是正三角形,所以CD⊥AB,又三棱柱ABC-A1B1C1是直三棱柱,所以CD⊥AA1,因此CD⊥平面A1ABB1,于是∠CA1D为直线A1C与平面A1ABB1所成的角,由题设知∠CA1D=45°,
所以A1D=CD=![]() AB=
AB=![]() ,在Rt△AA1D中,AA1=
,在Rt△AA1D中,AA1=![]()
![]() ,所以FC=
,所以FC=![]() AA1=
AA1=![]() ,故三棱锥F-AEC的体积V=
,故三棱锥F-AEC的体积V=
![]() S△AEC×FC=
S△AEC×FC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,an>0,(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2.
(1)求数列{an}的通项公式;
(2)设bn=log2an , 数列{bn}的前n项和为Sn , 当 ![]() 最大时,求n的值.
最大时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,已知
中,已知![]() ,
,![]() (n∈N*)
(n∈N*)
(1)求数列![]() 的通项公式
的通项公式
(2)若![]() (λ为非零常数),问是否存在整数λ使得对任意n∈N*都有
(λ为非零常数),问是否存在整数λ使得对任意n∈N*都有![]() ?若存在,求出λ的值;若不存在,请说明理由.
?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,直线
,直线![]() 与
与![]() 的图象的相邻两个交点的横坐标分别是
的图象的相邻两个交点的横坐标分别是![]() 和
和![]() ,现有如下命题:
,现有如下命题:
①该函数在![]() 上的值域是
上的值域是![]() ;
;
②在![]() 上,当且仅当
上,当且仅当![]() 时函数取最大值;
时函数取最大值;
③该函数的最小正周期可以是![]() ;
;
④![]() 的图象可能过原点.
的图象可能过原点.
其中的真命题有__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2﹣7x+10<0,q:x2﹣4mx+3m2<0,其中m>0.
(1)若m=4,且p∧q为真,求x的取值范围;
(2)若¬q是¬p的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于155 ![]() 到195
到195![]() 之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,并按此分组绘制如图所示的频率分布直方图,其中第六组
,并按此分组绘制如图所示的频率分布直方图,其中第六组![]() 和第七组
和第七组![]() 还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
(1)补全频率分布直方图;
(2)根据频率分布直方图估计这50位男生身高的中位数;
(3)用分层抽样的方法在身高为![]() 内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在
内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=﹣sin2x+ ![]() 的图象,只需将y=sinxcosx的图象( )
的图象,只需将y=sinxcosx的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c,向量 ![]() =(a,c),
=(a,c), ![]() =(1﹣2cosA,2cosC﹣1),
=(1﹣2cosA,2cosC﹣1), ![]()
(Ⅰ)若b=5,求a+c值;
(Ⅱ)若 ![]() ,且角A是△ABC中最大内角,求角A的大小.
,且角A是△ABC中最大内角,求角A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某城市居民用水量的情况,我们获得100位居民某年的月均用水量(单位:吨)通过对数据的处理,我们获得了该100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏)
100位居民月均用水量的频率分布表
组号 | 分组 | 频数 | 频率 |
1 |
| 4 | 0.04 |
2 |
| 0.08 | |
3 |
| 15 | |
4 |
| 22 | |
5 |
|
| |
6 |
| 14 | 0.14 |
7 |
| 6 |
|
8 |
| 4 | 0.04 |
9 |
| 0.02 | |
合 计 | 100 | ||

(1)确定表中![]() 与
与![]() 的值;
的值;
(2)求频率分布直方图中左数第4个矩形的高度;
(3)在频率分布直方图中画出频率分布折线图;
(4)我们想得到总体密度曲线,请回答我们应该怎么做?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com