
【题目】在等比数列{an}中,an>0,(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2.
(1)求数列{an}的通项公式;
(2)设bn=log2an , 数列{bn}的前n项和为Sn , 当 ![]() 最大时,求n的值.
最大时,求n的值.
【答案】
(1)解:因为a1a5+2a3a5+a2a8=25,所以,a32+2a3a5+a52=25
又an>o,a3+a5=5,
又a3与a5的等比中项为2,所以,a3a5=4
而q∈(0,1),所以,a3>a5,所以,a3=4,a5=1,q= ![]() ,a1=16,
,a1=16,
所以,an=16× ![]() =25﹣n
=25﹣n
(2)解:bn=log2an=5﹣n,所以,bn+1﹣bn=﹣1,
所以,{bn}是以4为首项,﹣1为公差的等差数列
所以sn= ![]()
![]() =
= ![]()
所以,当n≤8时, ![]() >0,
>0,
当n=9时, ![]() =0,
=0,
n>9时, ![]() <0,
<0,
当n=8或9时, ![]() 最大
最大
【解析】(1)利用等比数列的性质把a1a5+2a3a5+a2a8=25转化为a32+2a3a5+a52=25,求出a3+a5=5,再利用a3与a5的等比中项为2即可首项和公比,进而求出数列{an}的通项公式;(2)先利用(1)求出数列{bn}的通项公式以及前n项和为Sn , ,进而得到 ![]() 的通项,即可求出当
的通项,即可求出当 ![]() 最大时,对应n的值.
最大时,对应n的值.
【考点精析】利用等差数列的性质对题目进行判断即可得到答案,需要熟知在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+21nx.
(1)求f(x)的单调区间.
(2)若f(x)在(0,1]上的最大值是﹣2,求a的值.
(3)记g(x)=f(x)+(a﹣1)lnx+1,当a≤﹣2时,若对任意x1 , x2∈(0,+∞),总有|g(x1)﹣g(x2)|≥k|x1﹣x2|成立,试求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:

(1)求该班全体男生的人数;
(2)求分数在![]() 之间的男生人数,并计算频率分布直方图中
之间的男生人数,并计算频率分布直方图中![]() 之间的矩形的高.
之间的矩形的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,﹣1),B(4,0),C(2,2),平面区域D是所有满足 ![]() =
= ![]() +μ
+μ ![]() (1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
(1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
A.5
B.4 ![]()
C.9
D.5+4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟,课后研讨20分钟,可获得学分5分B套选修课播32分钟,课后研讨40分钟,可获学分4分。全学期20周,网络每周开播两次,每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟,研讨时间不得少于1000分钟。两套选修课怎样合理选择,才能获得最好学分成绩?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式an;
(2)若a3 , a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}为等差数列,且a5=14,a7=20,数列{bn}的前n项和为Sn , b1= ![]() 且3Sn=Sn﹣1+2(n≥2,n∈N).
且3Sn=Sn﹣1+2(n≥2,n∈N).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=anbn , n=1,2,3,…,Tn为数列{cn}的前n项和,Tn<m对n∈N*恒成立,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
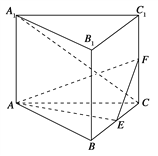
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com