
 |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,则
的夹角为60°,则 +
+ 在
在 方向上的投影为________.
方向上的投影为________. |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,算出|
的夹角为60°,算出| +
+ |=
|= 且(
且( +
+ )•
)• =2.再设
=2.再设 +
+ 与
与 的夹角为θ,结合数量积公式和向量投影的定义,算出|
的夹角为θ,结合数量积公式和向量投影的定义,算出| +
+ |cosθ的值,即可得到向量
|cosθ的值,即可得到向量 +
+ 在
在 方向上的投影值.
方向上的投影值. |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,
的夹角为60°, •
• =
= |×|
|×| |×cos60°=1
|×cos60°=1 +
+ )2=|
)2=| |2+2
|2+2 •
• +|
+| |2=1+2+4=7
|2=1+2+4=7 +
+ |=
|= .设
.设 +
+ 与
与 的夹角为θ,则
的夹角为θ,则 +
+ )•
)• =|
=| |2+
|2+ •
• =2
=2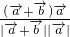 =
=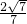 ,
, +
+ 在
在 方向上的投影为|
方向上的投影为| +
+ |cosθ=
|cosθ= ×
×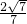 =2
=2 |、|
|、| |和
|和 与
与 的夹角,求向量
的夹角,求向量 +
+ 在
在 方向上的投影.着重考查了向量数量积的定义、向量的夹角公式和向量投影的概念等知识,属于基础题.
方向上的投影.着重考查了向量数量积的定义、向量的夹角公式和向量投影的概念等知识,属于基础题. 

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
| ∫ | 1 -1 |
| ∫ | t 0 |
| A、-6 | B、-12 | C、4 | D、-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com