
【题目】下列说法中,正确的有_______.(写出所有正确说法的序号)
①在![]() 中,若
中,若![]() ,则
,则![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形;
是锐角三角形;
③在![]() 中,若
中,若![]() ,则
,则![]() ;
;
④若![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,则三点
,则三点![]()
![]()
![]() 共线;
共线;
⑤等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,点
,点![]() 均在函数
均在函数![]() (
(![]() 且
且![]() ,
,![]()
![]() 均为常数)的图象上,则
均为常数)的图象上,则![]() 的值为
的值为.
【答案】①③④⑤
【解析】
根据正弦定理及边角关系可判断①;根据正弦定理及余弦定理,可判断角![]() 为锐角,但不能判断角
为锐角,但不能判断角![]() 和角
和角![]() 的情况,因而②错误;结合正弦定理及余弦定理可判断角
的情况,因而②错误;结合正弦定理及余弦定理可判断角![]() 为钝角,结合正切的和角公式,变形后即可判断③;根据等差数列前n项和的性质,结合两点间的斜率公式,可判断④;将点带入函数解析式,结合
为钝角,结合正切的和角公式,变形后即可判断③;根据等差数列前n项和的性质,结合两点间的斜率公式,可判断④;将点带入函数解析式,结合![]() 求得通项公式,结合等比数列的定义即可求得
求得通项公式,结合等比数列的定义即可求得![]() .
.
对于①,在![]() 中,若
中,若![]() ,则由大角对大边可知
,则由大角对大边可知![]() .设
.设![]() 外接圆半径为
外接圆半径为![]() ,由正弦定理可知
,由正弦定理可知![]() ,即
,即![]() .所以①正确;
.所以①正确;
对于②,在![]() 中,若
中,若![]() ,由正弦定理可得
,由正弦定理可得![]() ,可判定角
,可判定角![]() 为锐角.但当角
为锐角.但当角![]() 或角
或角![]() 为钝角时也成立,因而不能说明是锐角三角形,所以②错误.
为钝角时也成立,因而不能说明是锐角三角形,所以②错误.
对于③,在![]() 中,若
中,若![]() ,由正弦定理可知
,由正弦定理可知![]() ,则
,则![]() ,所以角
,所以角![]() 为钝角.由正切和角公式可知,
为钝角.由正切和角公式可知,![]() ,
,
所以![]()
![]()
![]()
所以![]()
因为角![]() 为钝角,所以角
为钝角,所以角![]() 和角
和角![]() 必为锐角,因而
必为锐角,因而![]() ,所以
,所以![]() ,所以③正确;
,所以③正确;
对于④,![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,则由等差数列前
,则由等差数列前![]() 项和公式可得
项和公式可得![]() ,则
,则![]() .所以
.所以![]() ,
,![]() ,
,![]()
由两点间斜率公式可得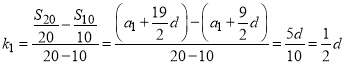

由![]() 可知三点共线,所以④正确;
可知三点共线,所以④正确;
对于⑤,点![]() 均在函数
均在函数![]() (
(![]() 且
且![]() ,
,![]()
![]() 均为常数)的图象上.
均为常数)的图象上.
则![]()
所以当![]() 时,
时,![]()
当![]() 时,
时,![]()
因为![]() 为等比数列,则首项也满足通项公式,所以
为等比数列,则首项也满足通项公式,所以![]()
解得![]() ,所以⑤正确.
,所以⑤正确.
综上可知,正确的为①③④⑤
故答案为: ①③④⑤


科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,雾霾的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题,某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律,每生产该型号空气净化器![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)求利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】篮球场上有5个人在练球,其战术是由甲开始发球(第1次传球),经过6次传球跑动后(中途每人的传接球机会均等),回到甲,由甲投3分球,其不同的传球方式有( )种.
A. 4 100 B. 1 024 C. 976 D. 820
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]() ,将
,将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若对任意![]() ,当
,当![]() 时,都有
时,都有![]() ,求实数
,求实数![]() 的最大值;
的最大值;
(3)若对任意实数![]() 在
在![]() 上与直线
上与直线![]() 的交点个数不少于6个且不多于10个,求实数
的交点个数不少于6个且不多于10个,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四边形ABCD,∠BAC=![]() ,AB=AC=2
,AB=AC=2![]() ,BD=CD=6,且平面ABC⊥平面BCD,则空间四边形ABCD的外接球的表面积为( )
,BD=CD=6,且平面ABC⊥平面BCD,则空间四边形ABCD的外接球的表面积为( )
A. 60π B. 36π C. 24π D. 12π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:
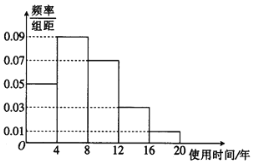
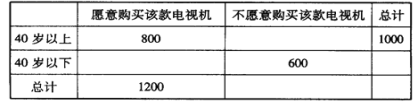
并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在[0,4)和[4,20]的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在[4,20]内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴顺时针滚动一周,设顶点
轴顺时针滚动一周,设顶点![]() 的运动轨迹与
的运动轨迹与![]() 轴所围区域为
轴所围区域为![]() ,若在平面区域
,若在平面区域![]() 内任意取一点
内任意取一点![]() ,则所取的点
,则所取的点![]() 恰好落在区域
恰好落在区域![]() 内部的概率为
内部的概率为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com