
【题目】已知圆![]() ,直线
,直线![]() ,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
(1)求E的方程;
(2)若点A,B是E上的两个动点,O为坐标原点,且![]() ,求证:直线AB恒过定点.
,求证:直线AB恒过定点.
科目:高中数学 来源: 题型:
【题目】党的“十八大”之后,做好农业农村工作具有特殊重要的意义.国家为了更 好地服务于农民、开展社会主义新农村工作,派调查组到农村某地区考察.该地区有100户农 民,且都从事蔬菜种植.据了解,平均每户的年收入为6万元.为了调整产业结构,当地政府决 定动员部分农民从事蔬菜加工.据统计,若动员![]() 户农民从事蔬菜加工,则剩下的继续 从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续 从事蔬菜种植的农民平均每户的年收入有望提高![]() ,而从事蔬菜加工的农民平均每户的年收入为
,而从事蔬菜加工的农民平均每户的年收入为![]() 万元.
万元.
(1)在动员![]() 户农民从事蔬菜加工后,要使剩下
户农民从事蔬菜加工后,要使剩下![]() 户从事蔬菜种植的所有农民总年收 入不低于动员前100户从事蔬菜种植的所有农民年总年收入,求
户从事蔬菜种植的所有农民总年收 入不低于动员前100户从事蔬菜种植的所有农民年总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这![]() 户农民从事蔬菜加工的总年收入始终不高于
户农民从事蔬菜加工的总年收入始终不高于![]() 户从事蔬菜种植的所有农民年总年收入,求
户从事蔬菜种植的所有农民年总年收入,求![]() 的最大值.(参考数据:
的最大值.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的五个区域中,中心区![]() 域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )
域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )

A. 56 B. 72 C. 64 D. 84
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院治疗白血病有甲、乙两套方案,现就70名患者治疗后复发的情况进行了统计,得到其等高条形图如图所示(其中采用甲、乙两种治疗方案的患者人数之比为![]() ).
).
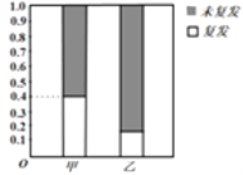
(1)补充完整![]() 列联表中的数据,并判断是否有
列联表中的数据,并判断是否有![]() 的把握认为甲、乙两套治疗方案对患者白血病复发有影响;
的把握认为甲、乙两套治疗方案对患者白血病复发有影响;
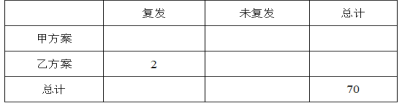
(2)从复发的患者中抽取3人进行分析,求其中接受“乙方案”治疗的人数![]() 的数学期望.
的数学期望.
附:
|
|
|
|
|
|
|
|
|
|
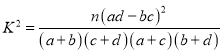 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com