
【题目】如图,在长方体![]() 中,
中,![]() 、
、![]() 分别是棱
分别是棱![]() ,
,![]()
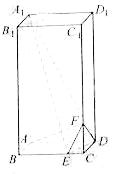
上的点,![]() ,
,![]()
(1) 求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2) 证明![]()
![]() 平面
平面![]()
![]()
(3) 求二面角![]() 的正弦值.
的正弦值.
【答案】(1)![]() ,(2)见解析(3)
,(2)见解析(3)![]()
【解析】
方法一:如图所示,建立空间直角坐标系,
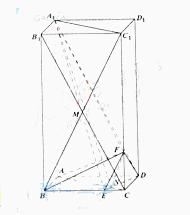
点A为坐标原点,设![]() ,依题意得
,依题意得![]() ,
,
![]() ,
,![]() ,
,![]()
(1) 解:易得![]() ,
,![]()
于是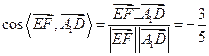
所以异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]()
(2) 证明:已知![]() ,
,![]() ,
,![]()
于是![]() ·
·![]() =0,
=0,![]() ·
·![]() =0.因此,
=0.因此,![]() ,
,![]() ,又
,又![]()
所以![]() 平面
平面![]()
(3)解:设平面![]() 的法向量
的法向量![]() ,则
,则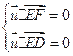 ,即
,即
不妨令X=1,可得![]() .由(2)可知,
.由(2)可知,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
于是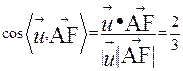 ,从而
,从而![]()
所以二面角![]() 的正弦值为
的正弦值为![]()
方法二:(1)解:设AB=1,可得AD=2,AA1=4,CF=1.CE=![]()
链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由![]() ,可知EF∥BC1.故
,可知EF∥BC1.故![]() 是异面直线EF与A1D所成的角,易知BM=CM=
是异面直线EF与A1D所成的角,易知BM=CM=![]() ,所以
,所以![]() ,所以异面直线FE与A1D所成角的余弦值为
,所以异面直线FE与A1D所成角的余弦值为![]()
(2)证明:连接AC,设AC与DE交点N 因为![]() ,所以
,所以![]() ,从而
,从而![]() ,又由于
,又由于![]() ,所以
,所以![]() ,故AC⊥DE,又因为CC1⊥DE且
,故AC⊥DE,又因为CC1⊥DE且![]() ,所以DE⊥平面ACF,从而AF⊥DE.
,所以DE⊥平面ACF,从而AF⊥DE.
连接BF,同理可证B1C⊥平面ABF,从而AF⊥B1C,所以AF⊥A1D因为![]() ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED
(3)解:连接A1N.FN,由(2)可知DE⊥平面ACF,又NF![]() 平面ACF, A1N
平面ACF, A1N![]() 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故![]() 为二面角A1-ED-F的平面角
为二面角A1-ED-F的平面角
易知![]() ,所以
,所以![]() ,又
,又![]() 所以
所以![]() ,在
,在![]()
![]()
连接A1C1,A1F 在![]()
![]() .所以
.所以![]()
所以二面角A1-DE-F正弦值为![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】根据教育部高考改革指导意见,广东省从2021年正式实施“![]() ”新的高考考试方案.为尽快了解学生的选科需求,及时调整学校人力资源配备.某校从高一学生中抽样调查了100名同学,在模拟分科选择中,一半同学(其中男生38人)选择了物理,另一半(其中男生14人)选择了历史.请完成以下
”新的高考考试方案.为尽快了解学生的选科需求,及时调整学校人力资源配备.某校从高一学生中抽样调查了100名同学,在模拟分科选择中,一半同学(其中男生38人)选择了物理,另一半(其中男生14人)选择了历史.请完成以下![]() 列联表,并判断能否有99.9%的把握说选科与性别有关?
列联表,并判断能否有99.9%的把握说选科与性别有关?
参考公式: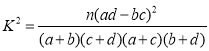 ,其中
,其中![]() 为样本容量.
为样本容量.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | |||
选物理 | 选历史 | 总计 | ||||||||
男生 | ||||||||||
女生 | ||||||||||
总计 | ||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如下表所示:
(天)之间的关系如下表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请根据上表数据在下列网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留三位小数);(注:
保留三位小数);(注: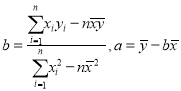 )
)
(3)在表格中(![]() 的8个对应点中,任取3个点,记这3个点在直线
的8个对应点中,任取3个点,记这3个点在直线![]() 的下方的个数为
的下方的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天,两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.经统计,两个厂家10天的试销情况茎叶图如下:

(Ⅰ)现从厂家试销的10天中抽取两天,求这两天的销售量都大于40的概率;
(Ⅱ)若将频率视作概率,回答以下问题:
(ⅰ)记乙厂家的日返利额为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(ⅱ)商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场做出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
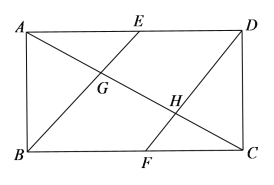
【题目】如图,一张矩形白纸![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,现分别将
的中点,现分别将![]() ,
,![]() 沿
沿![]() ,DF折起,且
,DF折起,且![]() 、
、![]() 在平面
在平面![]() 同侧,下列命题正确的是_________(写出所有正确命题的序号)
同侧,下列命题正确的是_________(写出所有正确命题的序号)
①平面![]() 平面
平面![]() 时,
时,![]()
②当平面![]() 平面
平面![]() 时,
时,![]() 平面
平面![]()
③当![]() 、
、![]() 重合于点
重合于点![]() 时,
时,![]()
④当![]() 、
、![]() 重合于点
重合于点![]() 时,三棱锥
时,三棱锥![]() 的外接球的半径为
的外接球的半径为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
(1)求E的方程;
(2)若点A,B是E上的两个动点,O为坐标原点,且![]() ,求证:直线AB恒过定点.
,求证:直线AB恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com