
分析 若p∨q”为真,p∧q为假,则p,q一真一假,进而答案.
解答 解:对于P:$\left\{{\begin{array}{l}{△>0}\\{{x_1}+{x_2}<0}\\{{x_1}{x_2}>0}\end{array}}\right.$,则得k>4(2分)
对于q:把圆的方程化为标准方程得(x+$\frac{k}{2}$)2+(y+1)2=16-$\frac{3k2}{4}$
所以16-$\frac{3k2}{4}$>0,解得-$\frac{8\sqrt{3}}{3}$<k<$\frac{8\sqrt{3}}{3}$.
由题意知点(1,2)应在已知圆的外部,
把点代入圆的方程得1+4+k+4+k2-15>0,
即(k-2)(k+3)>0,解得k>2或k<-3,
则实数k的取值范围是-$\frac{8\sqrt{3}}{3}$<k<-3,或2<k<$\frac{8\sqrt{3}}{3}$.(7分)
若p∨q”为真,p∧q为假,则p,q一真一假
(1)p为真,q为假时,易得k∈(4,+∞).(9分)
(2)p为假,q为真时,易得$k∈(-\frac{8\sqrt{3}}{3},-3)∪(2,4]$(11分)
所以所求实数m的取值范围是$k∈(-\frac{8\sqrt{3}}{3},-3)∪(2,+∞)$(12分)
点评 本题以命题的真假判断与应用为载体,考查了复合命题,方程根的个数,直线与圆的位置关系等知识点,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 设p:f(x)=x3+2x2+mx+1是R上的单调增函数,$q:m≥\frac{4}{3}$,则p是q的必要不充分条件 | |
| B. | 若命题$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则¬p:?x∈R,x2-x+1>0 | |
| C. | 奇函数f(x)定义域为R,且f(x-1)=-f(x),那么f(8)=0 | |
| D. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
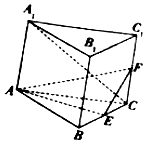 如图直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,E、F分别是BC,CC1的中点,
如图直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,E、F分别是BC,CC1的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com