
分析 (1)根据异面直线的距离的定义结合三棱锥的体积公式进行求解即可.
(2)找出异面直线AB,CD的公垂线,结合三棱锥的体积公式进行证明即可.
(3)根据锥体的体积公式进行求解.
解答 证明:(1)如图5-2,由于棱AB⊥平面BCD,过B作CD边上的高BE,
则AB⊥BE,CD⊥BE,
故BE是异面直线AB与CD的距离,即d=BE.
所以VA-BCD=$\frac{1}{3}$AB•S△BCD=$\frac{1}{3}$a$•\frac{1}{2}b•d$=$\frac{1}{6}$abd.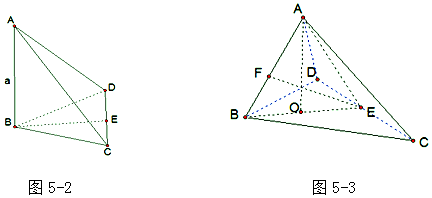
(2)如图5-3,过A作底面BCD的垂线,垂足为O,连结BO与CD相交于E.连结AE,
再过E作AB的垂线,垂足为F.
因为AB⊥CD,所以BO⊥CD(三垂线定理的逆定理),
所以CD⊥平面ABE,
因为EF?平面ABE,
所以CD⊥EF,
又EF⊥AB.
所以EF即为异面直线AB,CD的公垂线.
所以EF=d.注意到CD⊥平面ABE.
所以VA-BCD=$\frac{1}{3}$CD•S△ABE=$\frac{1}{3}$•$\frac{1}{2}$AB•EF•CD=$\frac{1}{6}$abd为定值.
(3)如图5-4:将四面体ABCD补成一个平行六面体ABB'D'-A'CC'D.
由于AB,CD所成角为θ,
所以∠DCA'=θ,
又异面直线AB与CD间的距离即上、下两底面AB',A'C'的距离,
所以VABB'D'-A'CC'D=$\frac{1}{2}$absinθ×2d=abdsinθ.
显然VA-BCD=$\frac{1}{6}$VABB'D'-A'CC'D=$\frac{1}{6}$abdsinθ.
点评 本题主要考查空间几何体的体积的计算,根据相应的体积公式以及异面直线的距离是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com