
分析 (1)求导数,利用f(x)与g(x)在x=1处相切,可求g(x)的表达式;
(2)$φ(x)=\frac{m(x-1)}{x+1}-f(x)$在[1,+∞)上是减函数,可得导函数小于等于0,在[1,+∞)上恒成立,分离参数,利用基本不等式,可求实数m的取值范围;
(3)当x≥2时,证明$2(\frac{1}{x-1}-\frac{1}{x})<\frac{1}{lnx}$,当x=2时,当x=3时,当x=4时,…,当x=n+1时,利用叠加法,即可得到结论.
解答 解:(1)∵f(x)=lnx,∴$f'(x)=\frac{1}{x}$,∴$f'(1)=1=\frac{1}{2}a$,得:a=2.
又∵$g(1)=0=\frac{1}{2}a+b$,∴b=-1,
∴g(x)=x-1;
(2)$φ(x)=\frac{m(x-1)}{x+1}-f(x)$=$\frac{m(x-1)}{x+1}-lnx$在[1,+∞)上是减函数,
∴$ϕ'(x)=\frac{{-{x^2}+(2m-2)x-1}}{{x{{(x+1)}^2}}}≤0$在[1,+∞)上恒成立.
即x2-(2m-2)x+1≥0在[1,+∞)上恒成立,由$2m-2≤x+\frac{1}{x}$,x∈[1,+∞),
∵$x+\frac{1}{x}∈[2,+∞)$,
∴2m-2≤2得m≤2;
证明:(3)由(1)可得:当x≥2时:$lnx<x-1≤\frac{x}{2}(x-1)$,∴$lnx<\frac{1}{2}x(x-1)$得:$\frac{2}{x(x-1)}<\frac{1}{lnx}$,
∴$2(\frac{1}{x-1}-\frac{1}{x})<\frac{1}{lnx}$.
当x=2时:$2(\frac{1}{1}-\frac{1}{2})<\frac{1}{ln2}$,
当x=3时:$2(\frac{1}{2}-\frac{1}{3})<\frac{1}{ln3}$,
当x=4时:$2(\frac{1}{3}-\frac{1}{4})<\frac{1}{ln4}$,
…
当x=n+1时:$2(\frac{1}{n}-\frac{1}{n+1})<\frac{1}{ln(n+1)}$,n∈N+,n≥2,
上述不等式相加得:$2(1-\frac{1}{n+1})<$$\frac{1}{ln2}+\frac{1}{ln3}+\frac{1}{ln4}+…+\frac{1}{ln(n+1)}$,
即:$\frac{2n}{n+1}<$$\frac{1}{ln2}+\frac{1}{ln3}+\frac{1}{ln4}+…+\frac{1}{ln(n+1)}$.
点评 本题考查利用导数研究曲线上某点的切线方程,考查利用导数研究函数的单调性,考查基本不等式的运用,考查叠加法,考查学生分析解决问题的能力,是中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 10 | 10 | 15 | A4 | A5 |
| B型数量(台) | 10 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p为假 | B. | p∧q为假 | C. | p∨q为真 | D. | ¬q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
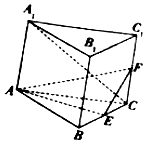 如图直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,E、F分别是BC,CC1的中点,
如图直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,E、F分别是BC,CC1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(1)<f(-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{{({x-1})}^2}}$,g(x)=x-1 | B. | f(x)=$\sqrt{{x^2}-1},g(x)=\sqrt{x-1}•\sqrt{x+1}$ | ||
| C. | f(x)=x-1,g(x)=$\frac{1}{x-1}$ | D. | f(x)=x0,g(x)=$\frac{1}{x^0}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com