
| ��һ�� | �ڶ��� | ������ | ������ | ������ | |
| A��������̨�� | 10 | 10 | 15 | A4 | A5 |
| B��������̨�� | 10 | 12 | 13 | B4 | B5 |
| C��������̨�� | 15 | 8 | 12 | C4 | C5 |
���� ��1�����������е���ֵ����ƽ�������ɣ�
��2������1�����ݸ��ʵĶ�����м��㼴�ɣ�
����2�����ö����¼��ĸ��ʹ�ʽ���м���Ҳ�ɣ�
��3�����ݷ���Ķ���ɵ�S2�Ľ���ʽ���ٸ��ݶ��κ����������
c4=7��c4=8ʱ��S2ȡ����Сֵ���Ӷ����c5��ֵ��
��� �⣺��1��A�Ϳյ�ǰ���ܵ�ƽ��������Ϊ
$\overline x=\frac{10+10+15}{3}=\frac{35}{3}$��̨��������2�֣�
��2������1����ǰ�����۳������пյ��������ȡһ̨����105�ֿ��ܣ�
���С���B�ͻ��ǵ�һ���۳��յ�����35+35-10=60������4�֣�
��˳鵽�Ŀյ�����B�ͻ��ǵ�һ���۳��յ����ĸ�����$P=\frac{60}{105}=\frac{4}{7}$������6�֣�
����2����鵽�Ŀյ�������B��Ҳ���ǵ�һ���۳��յ������¼���M��
�鵽�Ŀյ�����B�ͻ��ǵ�һ���۳��յ������¼���N��
��$P��M��=\frac{10+15+8+12}{35+30+40}=\frac{3}{7}$��
$P��N��=1-\frac{3}{7}=\frac{4}{7}$������4�֣�
�ʳ鵽�Ŀյ�����B�ͻ��ǵ�һ���۳��յ����ĸ�����$\frac{4}{7}$������6�֣�
��3����ΪC�Ϳյ�ƽ����������Ϊ10̨��
����c4+c5=10��5-15-8-12=15������8�֣�
��${s^2}=\frac{1}{5}[{��15-10��^2}+{��8-10��^2}+{��12-10��^2}+{��{c_4}-10��^2}+{��{c_5}-10��^2}]$��
�����${s^2}=\frac{1}{5}[2{��{c_4}-\frac{15}{2}��^2}+\frac{91}{2}]$������10�֣�
��Ϊc4��N��
����c4=7��c4=8ʱ��S2ȡ����Сֵ��
��ʱC5=8��C5=7����12�֣�
���� ���⿼���˸��ʵ����о�ƽ�����ͷ���ļ������⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q�� | B�� | p�� q�� | C�� | p��q�� | D�� | p��q�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
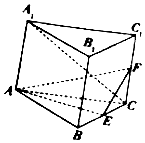 ��ͼֱ������ABC-A1B1C1�ĵ����DZ߳�Ϊ4���������Σ�E��F�ֱ���BC��CC1���е㣬
��ͼֱ������ABC-A1B1C1�ĵ����DZ߳�Ϊ4���������Σ�E��F�ֱ���BC��CC1���е㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com