
已知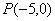 ,点
,点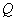 是圆
是圆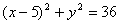 上的点,
上的点,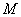 是线段
是线段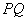 的中点.
的中点.
(Ⅰ)求点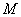 的轨迹
的轨迹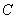 的方程.
的方程.
(Ⅱ)过点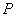 的直线
的直线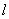 和轨迹
和轨迹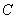 有两个交点
有两个交点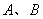 (
(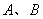 不重合),①若
不重合),①若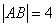 ,,求直线
,,求直线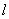 的方程.②求
的方程.②求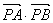 的值.
的值.
科目:高中数学 来源: 题型:
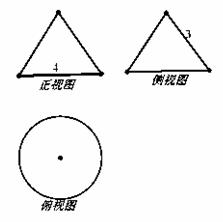
某工厂为了制造一个实心工件,先画出了这个工件的三视图(如图),其中正视图与侧视图为两个全等的等腰三角形,俯视图为一个圆,三视图尺寸如图所示(单位cm);
(1)求出这个工件的体积;
(2)工件做好后,要给表面喷漆,已知喷漆费用是每平方厘米1元,现要制作10个这样的工件,请计算喷漆总费用(精确到整数部分).
查看答案和解析>>
科目:高中数学 来源: 题型:
假设某人在任何时间到达某十字路口是等可能的,已知路口的红绿灯,红灯时间为40秒,黄灯时间为3秒,绿灯时间为57秒,则此人到达路口恰好是红灯的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
一位射击爱好者在一次射击练习中射靶100次,每次命中的环数如下表:
| 环数 | 6及以下 | 7 | 8 | 9 | 10 |
| 频数 | 18 | 32 | 22 | 13 | 15 |
据此估计他射击成绩在8环及8环以上的概率为 _________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
在长为12cm的线段AB上任取一点M,并以线段AM为一边作正方形,则此正方形的面积介于36cm2与81cm2之间的概率为( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com