
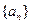 满足
满足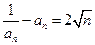 ,且
,且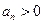 。
。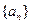 的通项公式;
的通项公式;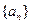 是否存在最大项?若存在最大项,求出该项和相应的项数;若不存在,说明理由。
是否存在最大项?若存在最大项,求出该项和相应的项数;若不存在,说明理由。 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
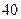 %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化. 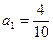 ,经过
,经过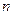 年后绿化的面积为
年后绿化的面积为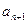 ,试用
,试用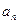 表示
表示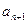 ;
;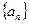 的第
的第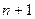 项
项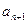 ;
;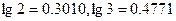 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
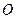 向三次曲线
向三次曲线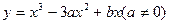 引切线,切于不同于点
引切线,切于不同于点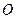 的点
的点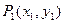 ,再由
,再由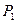 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于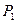 的点
的点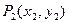 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列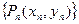 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求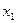 ; (2)求
; (2)求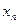 与
与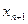 的关系式;
的关系式; 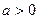 ,求证:当
,求证:当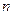 为正偶数时,
为正偶数时,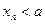 ;当
;当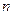 为正奇数时,
为正奇数时,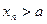 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com