
 向三次曲线
向三次曲线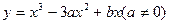 引切线,切于不同于点
引切线,切于不同于点 的点
的点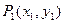 ,再由
,再由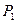 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于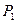 的点
的点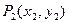 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列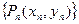 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求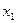 ; (2)求
; (2)求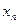 与
与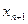 的关系式;
的关系式; 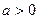 ,求证:当
,求证:当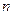 为正偶数时,
为正偶数时,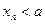 ;当
;当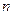 为正奇数时,
为正奇数时,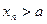 .
. 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:不详 题型:解答题
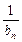 )(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与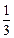 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
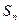 为数列
为数列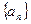 的前
的前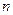 项和,
项和,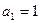 ,
,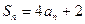 .
.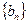 中,
中,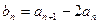 ,求证:
,求证: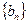 是等比数列;
是等比数列;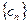 中,
中,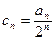 ,求证:
,求证: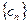 是等差数列;
是等差数列;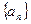 的通项公式及前
的通项公式及前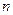 项和.
项和.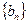 和
和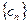 中的项与
中的项与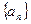 中的项有关,且
中的项有关,且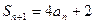 ,可利用
,可利用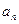 、
、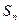 的关系作为切入点.
的关系作为切入点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com