
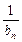 )(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与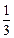 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.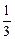 logabn+1;当0<a<1时,Sn<
logabn+1;当0<a<1时,Sn<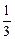 logabn+1
logabn+1
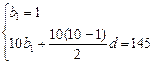
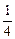 )+…+loga(1+
)+…+loga(1+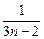 )
)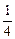 )…(1+
)…(1+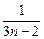 )],
)],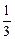 logabn+1=loga
logabn+1=loga .
.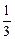 logabn+1的大小,
logabn+1的大小,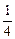 )…(1+
)…(1+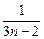 )与
)与 的大小,
的大小,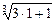
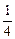 )>
)>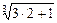 …
…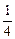 )…(1+
)…(1+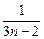 )>
)>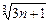 ①
①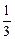 logabn+1, ②
logabn+1, ②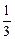 logabn+1, ③
logabn+1, ③
 那么当n=k+1时,
那么当n=k+1时,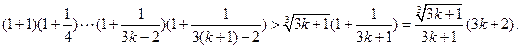

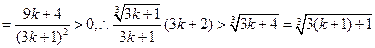
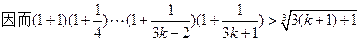

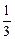 logabn+1;当0<a<1时,Sn<
logabn+1;当0<a<1时,Sn<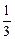 logabn+1
logabn+1

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
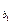 ,a
,a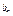 ,…,a
,…,a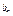 ,…为等比数列,其中b1=1,b2=5,b3=17.
,…为等比数列,其中b1=1,b2=5,b3=17.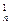 b1+C
b1+C b2+C
b2+C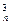 b3+…+C
b3+…+C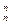 bn,求
bn,求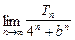 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 “2001年国内生产总值达到95933亿元,比上年增长7
“2001年国内生产总值达到95933亿元,比上年增长7 3%,”如果“十·五”期间(2001年~2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为_________亿元.
3%,”如果“十·五”期间(2001年~2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为_________亿元.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的定义域为
的定义域为 ,且对任意的正实数x,y有:
,且对任意的正实数x,y有: 且
且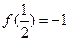 .
.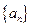 满足:
满足: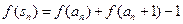 其中
其中 为数列
为数列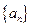 的前n项和,求数列
的前n项和,求数列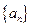 的通项公式;
的通项公式;
 成立?若存在,求出M的取值范围;若不存在,请说明理由.
成立?若存在,求出M的取值范围;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
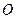 向三次曲线
向三次曲线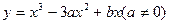 引切线,切于不同于点
引切线,切于不同于点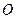 的点
的点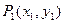 ,再由
,再由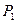 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于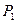 的点
的点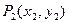 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列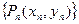 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求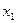 ; (2)求
; (2)求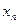 与
与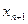 的关系式;
的关系式; 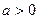 ,求证:当
,求证:当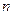 为正偶数时,
为正偶数时,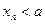 ;当
;当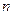 为正奇数时,
为正奇数时,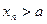 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com