
【题目】2018年9月16日下午5时左右,今年第22号台风“山竹”在广东江门川岛镇附近正面登陆,给当地人民造成了巨大的财产损失,某记者调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如下频率分布直方图.
五组,并作出如下频率分布直方图.
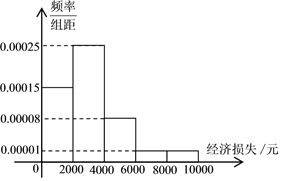
(Ⅰ)根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.
(Ⅱ)“一方有难,八方支援”,台风后居委会号召小区居民为台风重灾区捐款,![]() 记者调查的100户居民捐款情况如下表格,在表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
记者调查的100户居民捐款情况如下表格,在表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
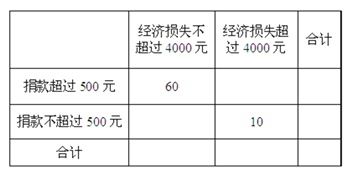
(Ⅲ)将上述调查所得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过![]() 元的人数为
元的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列及期望
的分布列及期望![]() .
.
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
【答案】(Ⅰ)众数为3000,平均值为2920(Ⅱ)没有把握(Ⅲ)详见解析
【解析】
(Ⅰ)最高矩形中点横坐标就是众数,每个矩形的中点横坐标与该矩形的纵坐标、组距相乘后求和可得平均值;(Ⅱ)根据直方图得到列联表,利用公式求得![]() ,与邻界值比较,即可得到结论;(Ⅲ)
,与邻界值比较,即可得到结论;(Ⅲ)![]() 的取值可能有
的取值可能有![]() ,根据独立重复试验概率公式求出各随机变量对应的概率,从而可得分布列,利用二项分布的期望公式可得结果.
,根据独立重复试验概率公式求出各随机变量对应的概率,从而可得分布列,利用二项分布的期望公式可得结果.
(Ⅰ)根据频率分布直方图知该小区居民由于台风造成的经济损失的众数=3000(元);
平均值=![]() (元)
(元)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,经济损失不超过![]() 元的有
元的有![]() 人,经济损失超过
人,经济损失超过![]() 元的有100-80=20人,
元的有100-80=20人,
则表格数据如下
经济损失不 超过4000元 | 经济损失超 过4000元 | 合计 | |
捐款超过500元 | 60 | 10 | 70 |
捐款不超过500元 | 20 | 10 | 30 |
合计 | 80 | 20 | 100 |
![]() .
.
由于![]() ,
,![]()
所以没有99%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
(Ⅲ)由频率分布直方图可知抽到自身经济损失超过![]() 元居民的频率为
元居民的频率为![]() ,将频率视为概率. 由题意知
,将频率视为概率. 由题意知![]() 的取值可能有
的取值可能有![]() ,
,
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的分布列
的分布列
![]()


科目:高中数学 来源: 题型:
【题目】已知![]() 和
和![]() 是椭圆
是椭圆![]() 的两个焦点,且点
的两个焦点,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)直线![]() (m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线
(m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某初级中学共有学生2000名,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
求x的值;
现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
已知y![]() 245,z
245,z![]() 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD="40" m,则电视塔的高度为多少?
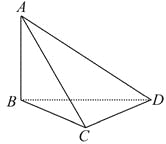
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数![]() ,定义域为
,定义域为![]() 的函数
的函数![]() 是偶函数,其中
是偶函数,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求实数![]() 值;
值;
(Ⅱ)判断该函数![]() 在
在![]() 上的单调性并用定义证明;
上的单调性并用定义证明;
(Ⅲ)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 恒成立.若存在,求出实数
恒成立.若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,其右焦点为
,其右焦点为![]() .点
.点![]() 是椭圆
是椭圆![]() 上异于长轴端点的任意一点,连接
上异于长轴端点的任意一点,连接![]() 并延长交椭圆
并延长交椭圆![]() 于点
于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且直线
为坐标原点,且直线![]() 与右准线
与右准线![]() 交于点
交于点![]() .
.
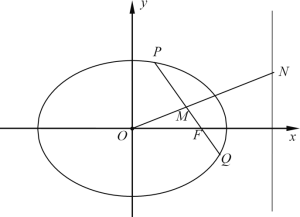
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 与
与![]() 的交点的轨迹
的交点的轨迹![]() 的方程;
的方程;
(2)若曲线![]() 上存在4个点到直线
上存在4个点到直线![]() 的距离相等,求实数
的距离相等,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com