
【题目】已知一圆的圆心![]() 在直线
在直线![]() 上,且该圆经过
上,且该圆经过![]() 和
和![]() 两点.
两点.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,试求
两点,试求![]() 面积的最大值和此时直线
面积的最大值和此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)最大值2,
(2)最大值2,![]() 或
或![]() .
.
【解析】
(1)方法一、求得![]() 的垂直平分线方程与已知直线联立,求得圆心,可得半径,即可得到所求圆的方程;
的垂直平分线方程与已知直线联立,求得圆心,可得半径,即可得到所求圆的方程;
方法二、设圆![]() 的方程为
的方程为![]() ,将点代入可得
,将点代入可得![]() ,
,![]() ,
,![]() 的方程组,解方程可得圆的方程;
的方程组,解方程可得圆的方程;
(2)直线![]() 与圆
与圆![]() 相交,设直线
相交,设直线![]() 的方程为
的方程为![]() ,求得圆心到直线的距离和弦长,由三角形的面积公式,化为关于
,求得圆心到直线的距离和弦长,由三角形的面积公式,化为关于![]() 的二次函数,求得最值,进而求得
的二次函数,求得最值,进而求得![]() ,可得所求直线方程;
,可得所求直线方程;
(1)方法一:![]() 和
和![]() 两点的中垂线方程为:
两点的中垂线方程为:![]() ,
,
圆心必在弦的中垂线上,联立![]() 得
得![]() ,
,
半径![]() ,所以圆
,所以圆![]() 的标准方程为:
的标准方程为:![]() .
.
方法二:设圆![]() 的标准方程为:
的标准方程为:![]() ,
,
由题得: ,解得:
,解得:![]()
所以圆![]() 的标准方程为:
的标准方程为:![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ,
,
![]() 面积
面积![]() ,
,
![]() 当
当![]() ,
,![]() 时,
时,![]() 取得最大值2
取得最大值2
此时![]() ,解得:
,解得:![]() 或
或![]()
所以,直线![]() 的方程为:
的方程为:![]() 或
或![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感车天地关于某品牌汽车的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (千元)由如表的统计资料:
(千元)由如表的统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
(1)画出散点图并判断使用年限与所支出的维修费用是否线性相关;如果线性相关,求回归直线方程;
(2)若使用超过8年,维修费用超过1.5万元时,车主将处理掉该车,估计第10年年底时,车主是否会处理掉该车?
( )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() ,对任意正整数
,对任意正整数![]() ,总存在正数
,总存在正数![]() 使得
使得![]() ,
, ![]() 恒成立:数列
恒成立:数列![]() 的前
的前![]() 项和
项和![]() ,且对任意正整数
,且对任意正整数![]() ,
, ![]() 恒成立.
恒成立.
(1)求常数![]() 的值;
的值;
(2)证明数列![]() 为等差数列;
为等差数列;
(3)若![]() ,记
,记![]()
![]() ,是否存在正整数
,是否存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,
, ![]() 恒成立,若存在,求正整数
恒成立,若存在,求正整数![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率为80%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4,5,6,7,8表示命中,9,0表示未命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
据此估计,该运动员三次投篮均命中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与直线
两点,与直线![]() 相交于点
相交于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对某小区30位居民的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的,饮食以肉类为主).

(1)根据茎叶图,说明这30位居民中50岁以上的人的饮食习惯;
(2)根据以上数据完成如下2×2列联表;
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(3)能否有99%的把握认为居民的饮食习惯与年龄有关?
独立性检验的临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月16日下午5时左右,今年第22号台风“山竹”在广东江门川岛镇附近正面登陆,给当地人民造成了巨大的财产损失,某记者调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如下频率分布直方图.
五组,并作出如下频率分布直方图.
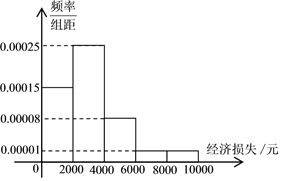
(Ⅰ)根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.
(Ⅱ)“一方有难,八方支援”,台风后居委会号召小区居民为台风重灾区捐款,![]() 记者调查的100户居民捐款情况如下表格,在表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
记者调查的100户居民捐款情况如下表格,在表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
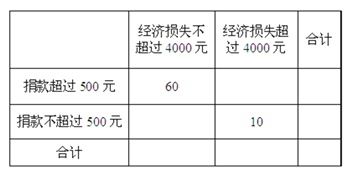
(Ⅲ)将上述调查所得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过![]() 元的人数为
元的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列及期望
的分布列及期望![]() .
.
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com