
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() ,对任意正整数
,对任意正整数![]() ,总存在正数
,总存在正数![]() 使得
使得![]() ,
, ![]() 恒成立:数列
恒成立:数列![]() 的前
的前![]() 项和
项和![]() ,且对任意正整数
,且对任意正整数![]() ,
, ![]() 恒成立.
恒成立.
(1)求常数![]() 的值;
的值;
(2)证明数列![]() 为等差数列;
为等差数列;
(3)若![]() ,记
,记![]()
![]() ,是否存在正整数
,是否存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,
, ![]() 恒成立,若存在,求正整数
恒成立,若存在,求正整数![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
【答案】(1)![]() (2)见解析(3)正整数
(2)见解析(3)正整数![]() 的最小值为4
的最小值为4
【解析】试题分析:(1)根据![]() ,
, ![]() ,可得
,可得![]() ,根据题意令
,根据题意令![]() 和
和![]() ,即可求出
,即可求出![]() ,从而求出
,从而求出![]() ;(2)由
;(2)由![]() ,得
,得![]() ,两式做差得
,两式做差得![]() ,从而可证数列
,从而可证数列![]() 为等差数列;(3)根据(2)可得
为等差数列;(3)根据(2)可得![]() ,结合(1),表示出
,结合(1),表示出![]() ,作出
,作出![]() ,然后令
,然后令![]() ,即可求出
,即可求出![]() 的最大值,从而求出正整数
的最大值,从而求出正整数![]() 的最小值.
的最小值.
试题解析:(1)∵![]() ①
①
∴![]() ②,
②,![]() ,
,
①-②得: ![]() ,即
,即![]() ,
, ![]() ,
,
又![]()
∴![]() ,
, ![]() ,
,
![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .
.
∵![]() 为正数
为正数
∴![]() .
.
又∵![]() ,
, ![]() ,且
,且![]()
∴![]() .
.
(2)∵![]() ③
③
∴当![]() 时,
时, ![]() ④,
④,
∴③-④得: ![]() ,即
,即![]() ⑤,
⑤,
又∵![]() ⑥
⑥
∴⑤+⑥得: ![]() ,即
,即![]()
∴![]() 为等差数列.
为等差数列.
(3)∵![]() ,
, ![]() ,由(2)知
,由(2)知![]() 为等差数列
为等差数列
∴![]() .
.
又由(1)知![]() ,
,
∴![]()
![]() ,
,
又∵![]()
![]() ,
,
∴![]()
![]() ,
,
令![]() 得
得![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() 时,
时, ![]() ,即
,即![]() ,
,
∵![]() 时,
时, ![]() ,
, ![]()
∴![]() ,即
,即![]() .
.
此时![]() ,即
,即![]() ,
,
∴![]() 的最大值为
的最大值为![]()
若存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,
, ![]() 恒成立,则
恒成立,则![]() ,
,
∴正整数![]() 的最小值为4.
的最小值为4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,
,![]() (
(![]() 且
且![]() ).
).
(1)求![]() 的值;
的值;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 为等差数列?若存在,求出
为等差数列?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月18日至10月24日,中国共产党第十九次全国代表大会![]() 简称党的“十九大”
简称党的“十九大”![]() 在北京召开
在北京召开![]() 一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在
一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在![]() 内,按成绩分成5组:第1组
内,按成绩分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
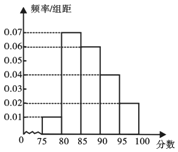
![]() 求这100人的平均得分
求这100人的平均得分![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 求第3,4,5组分别选取的作深入学习的人数;
求第3,4,5组分别选取的作深入学习的人数;
![]() 若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y.

(1)求抛物线在点P(2,1)处的切线方程;
(2)若不过原点的直线l与抛物线交于A,B两点(如图所示),且OA⊥OB,|OA|=![]() |OB|,求直线l的斜率.
|OB|,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD="40" m,则电视塔的高度为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com