
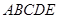 中,
中,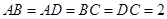 ,
,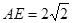 ,
,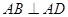 ,且
,且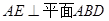 ,
,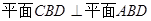 .
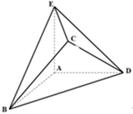
.
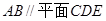 ;
;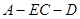 的余弦值.
的余弦值.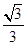 .
. 与
与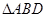 相似,从而得到
相似,从而得到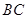 与
与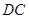 垂直,利用面面垂直的性质定理得
垂直,利用面面垂直的性质定理得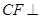 面
面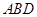 ,作出辅助线
,作出辅助线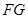 和
和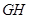 及
及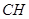 ,通过条件可得
,通过条件可得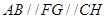 ,最后利用线面平行的判定证明
,最后利用线面平行的判定证明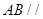 平面
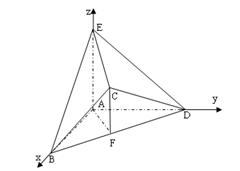
平面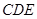 ;第二问,利用已知的垂直关系,建立如图的空间直角坐标系,写出各点的坐标,关键是求出平面
;第二问,利用已知的垂直关系,建立如图的空间直角坐标系,写出各点的坐标,关键是求出平面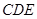 和平面
和平面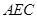 的法向量,利用夹角公式求出余弦值.
的法向量,利用夹角公式求出余弦值.
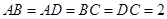
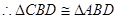 又
又
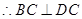 ,
,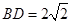
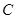 作
作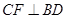 ,垂足为
,垂足为 ,则
,则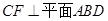 ,且
,且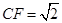 , 2分
, 2分 作
作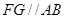 ,交
,交 于
于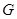 ,过
,过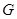 作
作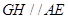 交
交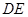 于
于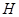 ,连结
,连结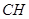 ,
,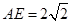 ,∴
,∴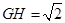 ,∴四边形
,∴四边形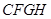 是平行四边形,
是平行四边形,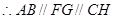 ,
,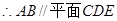 6分
6分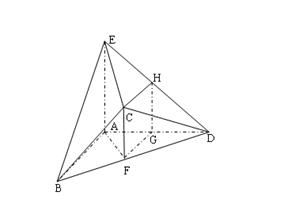
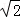 ),
),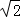 ),
),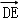 =(0,﹣2,2
=(0,﹣2,2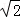 ),
),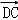 =(1,﹣1,
=(1,﹣1,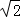 ), 8分
), 8分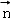 =(x,y,z),
=(x,y,z),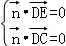 ,则﹣2y+2
,则﹣2y+2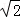 z=0,x﹣y+
z=0,x﹣y+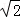 z=0,
z=0,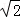 ,x=0,所以
,x=0,所以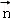 =(0,2
=(0,2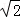 ,2), 10分
,2), 10分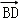 =(﹣2,2,0), 11分
=(﹣2,2,0), 11分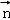 ,
,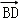 >=
>= 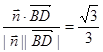 12分
12分

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源:不详 题型:解答题
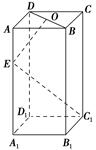
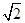 ,OE⊥EC1,求AA1的长.
,OE⊥EC1,求AA1的长.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
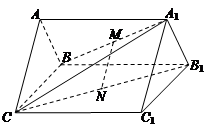
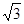 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.平面内的一条直线和这平面外的一条直线 |
| B.分别在不同平面内的两条直线 |
| C.不在同一个平面内的两条直线 |
| D.不同在任何一个平面内的两条直线. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com