
某公司计划2014年在A,B两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元.A,B两个电视台的广告收费标准分别为500元/分钟和200元/分钟,假定A,B两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在两个电视台做广告的时间,才能使公司的收益最大?最大收益是多少万元?
该公司在A电视台做100分钟广告,在B电视台做200分钟广告,公司的收益最大,最大收益是70万元.
【解析】设公司在A和B做广告的时间分别为x分钟和y分钟,总收益为z元,
由题意得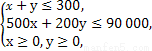
目标函数z=3000x+2000y.
二元一次不等式组等价于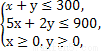
作出二元一次不等式组所表示的平面区域,即可行域,
如图阴影部分.
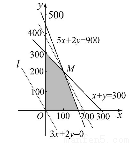
作直线l:3000x+2000y=0,即3x+2y=0,
平移直线l,从图中可知,当直线l过M点时,目标函数取得最大值.
联立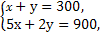
解得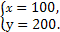
∴点M的坐标为(100,200),
∴zmax=3000×100+2000×200=700000,
即该公司在A电视台做100分钟广告,在B电视台做200分钟广告,公司的收益最大,最大收益是70万元.
【方法技巧】常见的线性规划应用题的类型
(1)给定一定量的人力、物力资源,问怎样运用这些资源,使完成的任务量最大,收益最大.
(2)给定一项任务,问怎样统筹安排,使完成这项任务耗费的人力、物力资源最小.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷(解析版) 题型:选择题
已知a>0,b>0,且2是2a与b的等差中项,则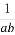 的最小值为( )
的最小值为( )
(A) (B)
(B) (C)2 (D)4
(C)2 (D)4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
设等差数列{an}的前n项和为Sn,则S4,S8-S4,S12-S8,S16-S12成等差数列,类比以上结论有:设等比数列{bn}的前n项积为Tn,则T4, , ,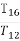 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:填空题
在数列{an}中,若对任意的n均有an+an+1+an+2为定值(n∈N*),且a7=2,a9=3,a98=4,则此数列{an}的前100项的和S100= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则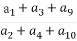 =( )
=( )
(A)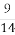 (B)
(B)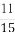 (C)
(C)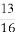 (D)
(D)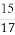
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:填空题
函数f(x)=x3+bx2+cx+d在区间[-2,2]上是减函数,则b+c的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
若不等式组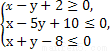 所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )
所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )
(A) (B)
(B) (C)
(C) (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:选择题
设等差数列{an}的前n项和为Sn,若S3=12,S6=42,则a10+a11+a12=( )
(A)156(B)102(C)66(D)48
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
以直角坐标系的原点为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l的极坐标方程为ρsin(θ-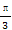 )=6,圆C的参数方程为
)=6,圆C的参数方程为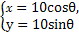 (θ为参数),求直线l被圆C截得的弦长.
(θ为参数),求直线l被圆C截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com