
函数f(x)=x3+bx2+cx+d在区间[-2,2]上是减函数,则b+c的最大值为 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十五第六章第一节练习卷(解析版) 题型:解答题
某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司要生产A类产品至少50件,B类产品至少140件,所需租赁费最多不超过2500元,写出满足上述所有不等关系的不等式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.有下列函数:
①f(x)=x+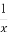 (x>0);②g(x)=x3;
(x>0);②g(x)=x3;
③h(x)=( )x;④φ()=lnx.
)x;④φ()=lnx.
其中是一阶整点函数的是( )
(A)①②③④ (B)①③④
(C)④ (D)①④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
等差数列{an}的前n项和为Sn,已知am-1+am+1-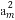 =0,S2m-1=38,则m=( )
=0,S2m-1=38,则m=( )
(A)38(B)20(C)10(D)9
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:解答题
某公司计划2014年在A,B两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元.A,B两个电视台的广告收费标准分别为500元/分钟和200元/分钟,假定A,B两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在两个电视台做广告的时间,才能使公司的收益最大?最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
已知x,y满足条件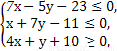 则
则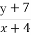 的取值范围是( )
的取值范围是( )
(A)[ ,9] (B)(-∞,
,9] (B)(-∞, )∪(9,+∞)
)∪(9,+∞)
(C)(0,9) (D)[-9,- ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:解答题
等差数列{an}的各项均为正数,其前n项和为Sn,满足2S2=a2(a2+1),且a1=1.
(1)求数列{an}的通项公式.
(2)设bn=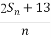 ,求数列{bn}的最小值项.
,求数列{bn}的最小值项.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷(解析版) 题型:解答题
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
API | 0~50 | 51~ 100 | 101~ 150 | 151~ 200 | 201~ 250 | 251~ 300 | >300 |
级 别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
状 况 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中度 重污染 | 重度 污染 |
|
|
|
|
|
| ||
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.
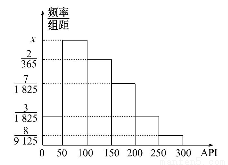
(1)求直方图中x的值.
(2)计算一年中空气质量分别为良和轻微污染的天数.
(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
(结果用分数表示.
已知57=78125,27=128,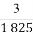 +
+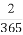 +
+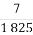 +
+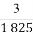 +
+ =
=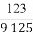 ,365=73×5).
,365=73×5).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
设直线l1的参数方程为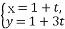 (t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.
(t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com