
设函数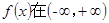 上满足以
上满足以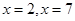 为对称轴,且在
为对称轴,且在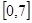 上只有
上只有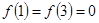 ,试求方程
,试求方程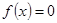 在
在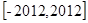 根的个数为( )
根的个数为( )
A、 803个 B、 804个 C、 805个 D、 806个
C
【解析】本试题主要是考查了函数与方程的思想的运用,求解零点问题的综合试题。
因为函数f(x)关于x=7对称可知f(x)=f(14-x),又因为关于x=2对称,那么可知f(x)=f(4-x)故有f(4-x)=f(14-x)⇒f(x)=f(x+10),周期为10,又f(3)=f(1)=0⇒f(11)=f(13)=f(-7)=f(-9)=0,因为在闭区间[0,7]上,只有f(1)=f(3)=0,故在[4,7]上无零点,又f(7-x)=f(7+x),故在[7,10]上无零点,故在[0,10]上仅有两个解,故f(x)在[0,10]和[-10,0]上均有有两个解,从而可知函数y=f(x)在[0,2012]上有403个解,在[-2012.0]上有400个解,所以函数y=f(x)在[-2012,2012]上有805个解.故选C.
解决该试题的关键是分析在闭区间[0,7]上,只有f(1)=f(3)=0,故在[4,7]上无零点,又f(7-x)=f(7+x),故在[7,10]上无零点,故在[0,10]上仅有两个解。然后利用周期性得到结论。


科目:高中数学 来源: 题型:
(本题满分13分)
已知函数![]()
(1)若![]() ,求曲线
,求曲线![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数![]() 上满足
上满足![]() ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有![]()
![]()
![]()
(1)试判断函数![]() 的奇偶性;
的奇偶性;
(2)试求方程![]() 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷七文科数学 题型:填空题
设函数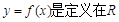 上的奇函数,且满足
上的奇函数,且满足 都成立,又
都成立,又
当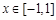 时,
时,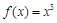 ,则下列四个命题:
,则下列四个命题:
①函数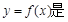 以4为周期的周期函数; ②当
以4为周期的周期函数; ②当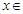 [1,3]时,
[1,3]时,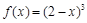 ;
;
③函数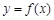 的图象关于
的图象关于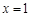 对称; ④函数
对称; ④函数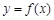 的图象关于点(2,0)对称.
的图象关于点(2,0)对称.
其中正确的命题序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年临沂高新区实验中学质检)设函数![]() 上的奇函数,且满足
上的奇函数,且满足![]() 都成立,又当
都成立,又当![]() 时,
时,![]() ,则下列四个命题:
,则下列四个命题:
①函数![]() 以4为周期的周期函数; ②当
以4为周期的周期函数; ②当![]() [1,3]时,
[1,3]时,![]() ;
;
③函数![]() 的图象关于x=1对称; ④函数
的图象关于x=1对称; ④函数![]() 的图象关于点(2,0)对称,
的图象关于点(2,0)对称,
其中正确的命题序号是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com