
已知函数 .
.
(1)当 且
且 时,证明:
时,证明: ;
;
(2)若对 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,证明:
时,证明: .
.
(1)详见解析;(2)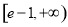 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)将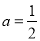 代入函数
代入函数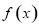 的解析式,构造新函数
的解析式,构造新函数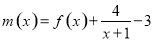 ,问题转化为证明
,问题转化为证明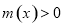 ,只需利用导数研究函数
,只需利用导数研究函数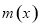 的单调性,利用函数
的单调性,利用函数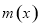 的单调性来证明该不等式;(2)解法一是利用参数分离法将不等式转化为
的单调性来证明该不等式;(2)解法一是利用参数分离法将不等式转化为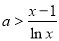 在
在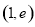 上恒成立,构造新函数
上恒成立,构造新函数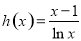 ,问题转化为
,问题转化为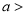
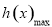 来处理;解法二是构造新函数
来处理;解法二是构造新函数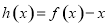 ,问题转化为
,问题转化为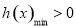 来处理,求出导数
来处理,求出导数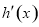 的根
的根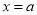 ,对
,对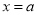 与区间
与区间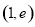 的相对位置进行分类讨论,以确定函数
的相对位置进行分类讨论,以确定函数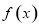 的单调性与最值,从而解决题中的问题;解法三是利用参数分离法将问题转化为
的单调性与最值,从而解决题中的问题;解法三是利用参数分离法将问题转化为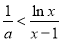 ,从而将问题转化为
,从而将问题转化为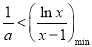 来处理,而将
来处理,而将 视为点
视为点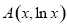 与点
与点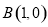 连线的斜率,然后利用图象确定
连线的斜率,然后利用图象确定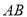 斜率的最小值,从而求解相应问题;(3)利用分析法将问题等价转化为证明不等式
斜率的最小值,从而求解相应问题;(3)利用分析法将问题等价转化为证明不等式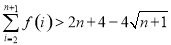 ,结合(1)中的结论
,结合(1)中的结论
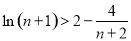 结合放缩法证明
结合放缩法证明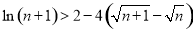 ,最后利用累加法证明相关不等式证明
,最后利用累加法证明相关不等式证明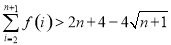 .
.
试题解析:(1)证明:要证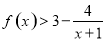 ,即证
,即证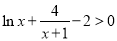 ,
,
令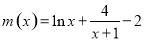 ,则
,则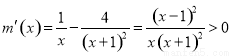 ,
,
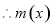 在
在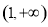 单调递增,
单调递增,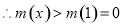 ,
,
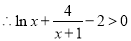 ,即
,即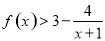 成立;
成立;
(2)解法一:由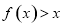 且
且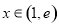 可得
可得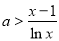 ,
,
令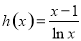 ,
, ,
,
由(1)知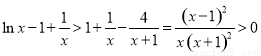 ,
,
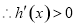 ,函数
,函数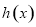 在
在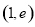 上单调递增,当
上单调递增,当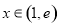 时,
时,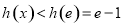 ,
,
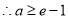 ;
;
解法二:令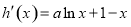 ,则
,则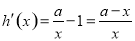 ,
,
当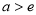 时,
时,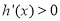 ,函数
,函数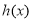 在
在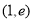 上是增函数,有
上是增函数,有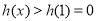 ,------6分
,------6分
当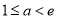 时,
时,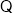 函数
函数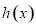 在
在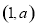 上递增,在
上递增,在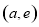 上递减,
上递减,
对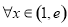 ,
,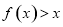 恒成立,只需
恒成立,只需 ,即
,即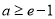 ;
;
当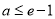 时,函数
时,函数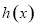 在
在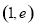 上递减,对
上递减,对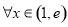 ,
,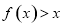 恒成立,只需
恒成立,只需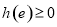 ,
,
而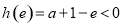 ,不合题意,
,不合题意,
综上得对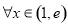 ,
,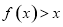 恒成立,
恒成立,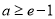 ;
;
解法三:由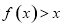 且
且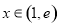 可得
可得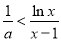 ,
,
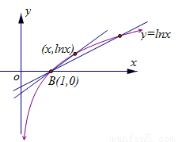
由于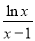 表示两点
表示两点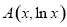 、
、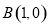 的连线斜率,
的连线斜率,
由图象可知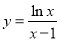 在
在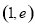 单调递减,
单调递减,
故当 ,
,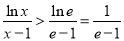 ,
,
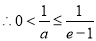 ,即
,即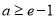 ;
;
(3)当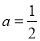 时,
时,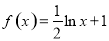 ,则
,则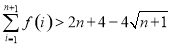 ,
,
要证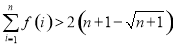 ,即证
,即证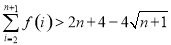 ,
,
由(1)可知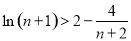 ,又
,又
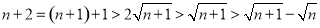 ,
,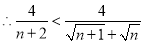 ,
,
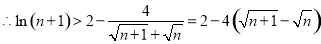 ,
,
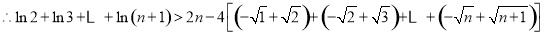
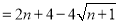 ,
,
故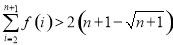 .
.
考点:1.利用导数证明函数不等式;2.参数分离法;3.直线的斜率;4.放缩法


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检理科数学试卷(解析版) 题型:选择题
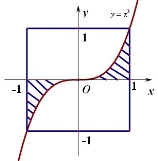
如图,设D是图中边长为2的正方形区域.,E是函数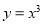 的图像与x轴及
的图像与x轴及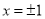 围成的阴影区域,项D中随机投一点,则该点落入E中的概率为( )
围成的阴影区域,项D中随机投一点,则该点落入E中的概率为( )
A.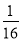 B.
B.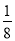 C.
C.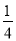 D.
D.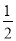
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试理科数学试卷(解析版) 题型:选择题
已知点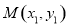 、
、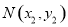 的坐标满足不等式组
的坐标满足不等式组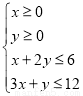 ,若
,若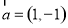 ,则
,则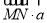 的
的
取值范围是( )
A.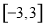 B.
B.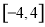 C.
C.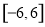 D.
D.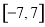
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数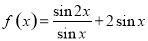 .
.
(1)求函数 的定义域和最小正周期;
的定义域和最小正周期;
(2)若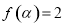 ,
,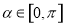 ,求
,求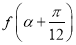 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试文科数学试卷(解析版) 题型:填空题
对于每一个正整数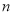 ,设曲线
,设曲线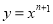 在点
在点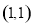 处的切线与
处的切线与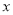 轴的交点的横坐标为
轴的交点的横坐标为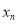 ,令
,令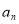
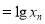 ,则
,则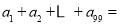 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:解答题
在平面直角坐标系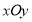 中,直线
中,直线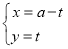 (
( 为参数)与圆
为参数)与圆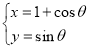 (
(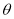 为参数)相切,切点在第一象限,则实数
为参数)相切,切点在第一象限,则实数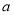 的值为.
的值为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com