
已知函数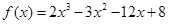 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若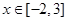 ,求函数
,求函数 的值域.
的值域.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
现有一张长为80 cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x(cm),高为y(cm),体积为V(cm3)
(1)求出x与 y的关系式;
(2)求该铁皮盒体积V的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某养殖厂需定期购买饲料,已知该厂每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该厂多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价的85%).问:该厂是否应考虑利用此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=ax2+x,若对任意x1、x2∈R,恒有2f ≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
(1)求函数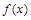 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(2)求函数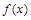 单调递增区间;
单调递增区间;
(3)若
 ∈[1,1],使得
∈[1,1],使得 (e是自然对数的底数),求实数
(e是自然对数的底数),求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数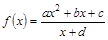 (其中
(其中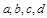 是实数常数,
是实数常数, )
)
(1)若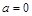 ,函数
,函数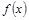 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求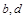 的值;
的值;
(2)若函数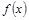 满足条件(1),且对任意
满足条件(1),且对任意 ,总有
,总有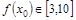 ,求
,求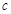 的取值范围;
的取值范围;
(3)若b=0,函数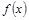 是奇函数,
是奇函数, ,
,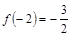 ,且对任意
,且对任意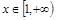 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数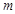 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)若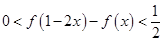 ,当
,当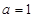 时,求
时,求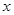 的取值范围;
的取值范围;
(2)若定义在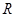 上奇函数
上奇函数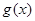 满足
满足 ,且当
,且当 时,
时,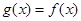 ,求
,求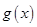 在
在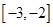 上的反函数
上的反函数 ;
;
(3)若关于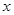 的不等式
的不等式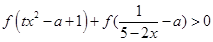 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设命题p:f(x)=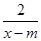 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若p∧q为真,试求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com