
【题目】已知函数f(x)=(x﹣1)2+a(lnx﹣x+1)(其中a∈R,且a为常数) (Ⅰ)当a=4时,求函数y=f(x)的单调区间;
(Ⅱ)若对于任意的x∈(1,+∞),都有f(x)>0成立,求a的取值范围;
(Ⅲ)若方程f(x)+a+1=0在x∈(1,2)上有且只有一个实根,求a的取值范围.
【答案】解:(1)函数f(x)的定义域为(0,+∞) 由 ![]() ,
,
当a=4时, ![]() ,
,
∴函数f(x)在(0,1)上单调递增,在(1,2)上单调递减,(2,+∞)在上单调递增;
(Ⅱ)由 ![]()
当a≤2时,
∵f'(x)>0对于x∈(1,+∞)恒成立,
∴f(x)在(1,+∞)上单调递增
∴f(x)>f(1)=0,此时命题成立;
当a>2时,
∵f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,
上单调递增,
∴当 ![]() 时,有f(x)<f(1)=0.这与题设矛盾,不合.
时,有f(x)<f(1)=0.这与题设矛盾,不合.
故a的取值范围是(﹣∞,2];
(Ⅱ)依题意,设g(x)=f(x)+a+1,
原题即为若g(x)在(1,2)上有且只有一个零点,求a的取值范围.
显然函数g(x)与f(x)的单调性是一致的.
当a≤0时,因为函数g(x)在(1,2)上递增,
由题意可知 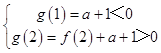 ,
,
解得 ![]() ;
;
当a>0时,因为g(x)=(x﹣1)2+alnx+(2﹣x)a+1,
当x∈(1,2)时,总有g(x)>0,此时方程没有实根.
综上所述,当 ![]() 时,方程f(x)+a+1=0在x∈(1,2)上有且只有一个实根.
时,方程f(x)+a+1=0在x∈(1,2)上有且只有一个实根.
【解析】(Ⅰ)根据导数和函数的单调性的关系即可求出,(Ⅱ)分类讨论,确定函数的单调性,从而解得;(Ⅲ)依题意,设g(x)=f(x)+a+1,原题即为若g(x)在(1,2)上有且只有一个零点,求a的取值范围.显然函数g(x)与f(x)的单调性是一致的,根据函数的单调性,当a<0,即可得到可知 ![]() ,解得即可,当a≥0,判断此时方程没有实根,问题得以解决.
,解得即可,当a≥0,判断此时方程没有实根,问题得以解决.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f′′(x)是f′(x)的导数,若方程f′′(x)有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,请你根据这一发现,计算f(
,请你根据这一发现,计算f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)﹣ ![]() x.
x.
(1)试判断函数f(x)的奇偶性并证明;
(2)设g(x)=log4(a2x﹣ ![]() a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据“2015年国民经济和社会发展统计公报” 中公布的数据,从2011 年到2015 年,我国的
第三产业在![]() 中的比重如下:
中的比重如下:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
第三产业比重 |
|
|
|
|
|
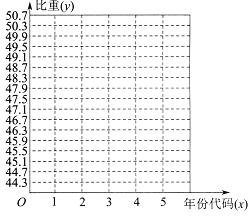
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在![]() 中的比重
中的比重![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在![]() 中的比重.
中的比重.
附注: 回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
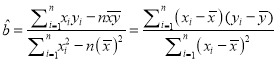 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列各组中两个函数是否为同一函数.
(1)f(x)=x2+2x﹣1,g(x)=t2+2t﹣1;
(2)f(x)=![]() , g(x)=x+1;
, g(x)=x+1;
(3)f(x)=![]()
![]() , g(x)=
, g(x)=![]() ;
;
(4)f(x)=|3﹣x|+1,g(x)=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 在
在![]() 单调递增,其中
单调递增,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,当
,当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小关系(其中
的大小关系(其中![]() 是
是![]() 的导函数),请写出详细的推理过程;
的导函数),请写出详细的推理过程;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足 ![]() ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com