【题目】已知函数f（x）=|x|﹣|2x﹣1|，记f（x）＞﹣1的解集为M．
（1）求M；
（2）已知a∈M，比较a2﹣a+1与 
的大小．
【答案】
（1）解：f（x）=|x|﹣|2x﹣1|=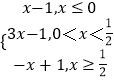 
，由f（x）＞﹣1，可得： 
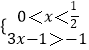或 
或 
，
解得0＜x＜2，∴M=（0，2）．
（2）解：由（1）知：0＜a＜2，∵a2﹣a+1﹣ 
= 
=g（a）．
当0＜a＜1时，g（a）＜0，∴a2﹣a+1＜ ；
当a=1时，g（a）=0，∴a2﹣a+1= ；
当1＜a＜2时，g（a）＞0，∴a2﹣a+1＞ ；
综上所述：当0＜a＜1时，∴a2﹣a+1＜ ；
当a=1时，a2﹣a+1= ；
当1＜a＜2时，a2﹣a+1＞
【解析】（1）f（x）=|x|﹣|2x﹣1|= 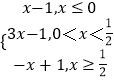，由f（x，由f（x）＞﹣1，可得： 
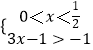或 
或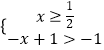 
，解出即可得出．（2）由（1）知：0＜a＜2，可得：a2﹣a+1﹣ = =g（a）．对a分类讨论：当0＜a＜1时，当a=1时，当1＜a＜2时，即可得出．
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=（x﹣1）2+a（lnx﹣x+1）（其中a∈R，且a为常数） （Ⅰ）当a=4时，求函数y=f（x）的单调区间；
（Ⅱ）若对于任意的x∈（1，+∞），都有f（x）＞0成立，求a的取值范围；
（Ⅲ）若方程f（x）+a+1=0在x∈（1，2）上有且只有一个实根，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|x|，g（x）=﹣|x﹣4|+m．
（1）解关于x的不等式g[f（x）]+3﹣m＞0；
（2）若函数f（x）的图象恒在函数g（2x）图象的上方，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若动点A，B分别在直线l1：x＋y－7＝0和l2：x＋y－5＝0上移动，则AB的中点M到原点的距离的最小值为( )
A.3 
B.2
C.3 
D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连接EC、CD．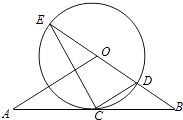 
（1）求证：直线AB是⊙O的切线；
（2）若tan∠CED= 
，⊙O的半径为3，求OA的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据要求，解答下列问题。
（1）求经过点A（3，2），B（-2，0）的直线方程；
（2）求过点P(-1，3),并且在两轴上的截距相等的直线方程；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，ABCD﹣A1B1C1D1是棱长为a的正方体，M、N分别是下底面的棱A1B1 ， B1C1的中点，P是上底面的棱AD上的一点，AP= 
，过P、M、N的平面交上底面于PQ，Q在CD上，则PQ= ．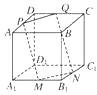 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
