已知集合U=R,集合A={x||x-a|<2},f(x)=2+log3x,x∈[1,9],设函数g(x)=[f(x)]2+f(x2)的值域为B,
(1)求值域B;
(2)若A⊆CUB,求实数a的取值范围.
【答案】
分析:(1)可由x∈[1,9],f(x)=2+log
3x,求得f(x)∈[1,4],从而可求得函数g(x)=[f(x)]
2+f(x
2)的值域为B;
(2)由B=[6,13]可求得)C
UB=(-∞,6)∪(13,+∞),A=(a-2,a+2),A⊆C
UB,从而可求得实数a的取值范围.
解答:解:∵A={x||x-a|<2},
∴-2<x-a<2,
∴a-2<x<2+a
∴A=(a-2,a+2)
∵x∈[1,9],故0≤log
3x≤2,
∴f(x)=(2+log
3x)∈[2,4],
∴f(x
2)=2+

,x
2∈[1,9],x∈[1,3],
∴函数g(x)=[f(x)]
2+f(x)的定义域为[1,3],
又
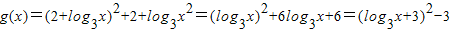
,
令t=log
3x,则0≤t≤1,
∴g(x)∈[6,13],即B=[6,13],
(2)∵C
UB=(-∞,6)∪(13,+∞),
A⊆C
UB,A=(a-2,a+2)
∴a+2≤6或a-2≥13.
∴a≤4或a≥15
点评:本题考查函数的值域,着重考查对数函数的性质与复合函数的性质,考查交、并、补集的混合运算,综合性强,属于难题.

 ,x2∈[1,9],x∈[1,3],
,x2∈[1,9],x∈[1,3],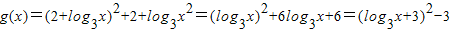 ,
,

 名校课堂系列答案
名校课堂系列答案